Pada artikel ini kita akan membahas materi Keliling dan Luas Segitiga . Untuk mempermudah dan melengkapi dalam mempelajarinya, baca juga materi lain yang bekaitan dengan segitiga yaitu "Jenis-jenis dan Sifat-sifat Segitiga" dan "Sudut-sudut pada Segitiga".
Contoh soal keliling dan luas segitiga :
1). Perhatikan segitiga berikut,
Pada $\Delta$DEF di atas diketahui DE = 14 cm, DF = 21 cm, EG = 5 cm, dan FG = 12 cm. Hitunglah keliling dan luas $\Delta$DEF.
Penyelesaian :
*). Pada segitiga EFG berlaku teorema pythagoras,
$ \begin{align} EF^2 & = EG^2 + GF^2 \\ EF & = \sqrt{EG^2 + GF^2 } \\ & = \sqrt{5^2 + 12^2 } \\ & = \sqrt{25 + 144 } \\ & = \sqrt{ 169 } \\ & = 13 \end{align} $
*). Keliling $\Delta$DEF
$ \begin{align} \text{Keliling } \Delta DEF & = DE + EF + FD \\ & = 14 + 13 + 21 \\ & = 48 \end{align} $
sehingga keliling $\Delta$DEF adalah 48 cm.
*). Menentukan luas $\Delta$DEF, alasnya DE = 14 dan tingginya FG = 12,
$ \begin{align} \text{Luas } \Delta DEF & = \frac{1}{2} \times DE \times FG \\ & = \frac{1}{2} \times 14 \times 12 \\ & = 7 \times 12 \\ & = 84 \end{align} $
Jadi, luas $\Delta$DEF adalah 84 cm$^2$.
2). Sebuah syal berbentuk segitiga sama kaki dengan panjang sisi yang sama 12 cm dan panjang sisi lainnya 30 cm. Jika tinggi syal tersebut 9 cm, tentukan
a). keliling syal;
b). luas syal.
Penyelesaian :
*). Gambar segitiganya untuk mewakili bentuk syalnya :
a). Keliling syal adalah keliling segitiga,
$ \begin{align} \text{Keliling } \Delta & = 12 + 12 + 30 \\ & = 54 \end{align} $
keliling syal adalah 54 cm.
b). Luas syal adalah luas segitiga,
$ \begin{align} \text{Luas } \Delta DEF & = \frac{1}{2} \times a \times t \\ & = \frac{1}{2} \times 30 \times 9 \\ & = 15 \times 9 \\ & = 135 \end{align} $
Jadi, luas syal adalah 135 cm$^2$.
3). Tentukan luas dua bangun datar berikut,
Penyelesaian :
*). Luas bangun datar gambar (a),
$ \begin{align} L_1 & = \frac{1}{2} \times 5 \times 8 \\ & = 20 \\ L_2 & = \frac{1}{2} \times 7 \times 6 \\ & = 21 \end{align} $
Luas bangun seluruhnya pada gambar (a),
Luas total $ = L_1 + L_2 = 20 + 21 = 41 \, $ dm$^2$ .
*). Luas bangun datar gambar (b),
$ \begin{align} L_1 & = L_{ABE} = \frac{1}{2} \times 13 \times 8 \\ & = 52 \\ L_2 & = L_{BDE} = \frac{1}{2} \times 5 \times 12 \\ & = 30 \\ L_3 & = L_{BCD} = \frac{1}{2} \times 3 \times 4 \\ & = 6 \end{align} $
Luas bangun seluruhnya pada gambar (b),
Luas total $ = L_1 + L_2 + L_3 = 52 + 30 + 6 = 88 \, $ cm$^2$ .
4). Diketahui luas sebuah segitiga adalah 165 cm$^2$ dan panjang alasnya 22 cm. Hitunglah tinggi segitiga.
Penyelesaian :
*). Diketahui : $ L = 165 \, $ dan $ a = 22 $.
*). Menentukan tinggi segitiga ($t$),
$ \begin{align} L & = 165 \\ \frac{1}{2} \times a \times t & = 165 \\ \frac{1}{2} \times 22 \times t & = 165 \\ 11 \times t & = 165 \\ t & = \frac{165}{11} = 15 \end{align} $
Jadi, tinggi segitiga adalah 15 cm.
Keliling Segitiga
Keliling suatu bangun datar merupakan jumlah dari semua sisi batas segitiga itu sendiri. Jadi untuk mencari keliling segitiga tersebut bisa dilakukan dengan penjumlahan semua sisi pada segitiga tersebut. . Perhatikan gambar segitiga ABC berikut,
$ \begin{align} \text{Keliling } \Delta \, ABC & = AB + BC + CD \\ & = a + b + c \end{align} $
Jadi, keliling segitiga ABC adalah $ a + b + c $.
$ \begin{align} \text{Keliling } \Delta \, ABC & = AB + BC + CD \\ & = a + b + c \end{align} $
Jadi, keliling segitiga ABC adalah $ a + b + c $.
Luas Segitiga
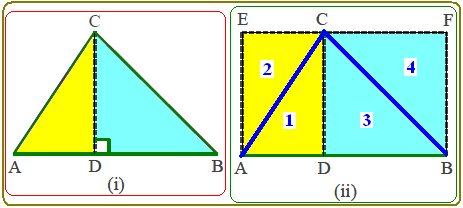
Perhatikan gambar segitiga ABC berikut ini,
*). Segitiga ABC pada gambar (i) kita bagi menjadi dua segitiga yang dipisah oleh garis tinggi (CD) yaitu segitiga ADC dan segitiga BDC.
*). Pada gambar (ii),
Luas $\Delta$ADC = $ \frac{1}{2} \, $ luas persegi panjang ADCE
$ \begin{align} \text{Luas } \Delta ADC & = \frac{1}{2} \times \text{ Luas persegi panjang ADCE} \\ & = \frac{1}{2} \times AD \times DC \\ \text{Luas } \Delta BDC & = \frac{1}{2} \times \text{ Luas persegi panjang BDCF} \\ & = \frac{1}{2} \times BD \times DC \end{align} $
*). Luas segitiga ABC adalah jumlah luas segitiga ADC dan segitiga BDC,
$ \begin{align} \text{Luas } \Delta ABC & = \text{Luas } \Delta ADC + \text{Luas } \Delta BDC \\ \text{Luas } \Delta ABC & = \frac{1}{2} \times AD \times DC + \frac{1}{2} \times BD \times DC \\ & = \frac{1}{2} \times DC \times (AD + BD) \\ & = \frac{1}{2} \times DC \times AB \end{align} $
dimana AB adalah sisi alas dan DC adalah tinggi segitiga.
Secara umum luas segitiga dengan panjang alas $ a \, $ dan tinggi $ t \, $ adalah
$ L = \frac{1}{2} \times a \times t $.
*). Segitiga ABC pada gambar (i) kita bagi menjadi dua segitiga yang dipisah oleh garis tinggi (CD) yaitu segitiga ADC dan segitiga BDC.
*). Pada gambar (ii),
Luas $\Delta$ADC = $ \frac{1}{2} \, $ luas persegi panjang ADCE
$ \begin{align} \text{Luas } \Delta ADC & = \frac{1}{2} \times \text{ Luas persegi panjang ADCE} \\ & = \frac{1}{2} \times AD \times DC \\ \text{Luas } \Delta BDC & = \frac{1}{2} \times \text{ Luas persegi panjang BDCF} \\ & = \frac{1}{2} \times BD \times DC \end{align} $
*). Luas segitiga ABC adalah jumlah luas segitiga ADC dan segitiga BDC,
$ \begin{align} \text{Luas } \Delta ABC & = \text{Luas } \Delta ADC + \text{Luas } \Delta BDC \\ \text{Luas } \Delta ABC & = \frac{1}{2} \times AD \times DC + \frac{1}{2} \times BD \times DC \\ & = \frac{1}{2} \times DC \times (AD + BD) \\ & = \frac{1}{2} \times DC \times AB \end{align} $
dimana AB adalah sisi alas dan DC adalah tinggi segitiga.
Secara umum luas segitiga dengan panjang alas $ a \, $ dan tinggi $ t \, $ adalah
$ L = \frac{1}{2} \times a \times t $.
1). Perhatikan segitiga berikut,
Pada $\Delta$DEF di atas diketahui DE = 14 cm, DF = 21 cm, EG = 5 cm, dan FG = 12 cm. Hitunglah keliling dan luas $\Delta$DEF.
Penyelesaian :
*). Pada segitiga EFG berlaku teorema pythagoras,
$ \begin{align} EF^2 & = EG^2 + GF^2 \\ EF & = \sqrt{EG^2 + GF^2 } \\ & = \sqrt{5^2 + 12^2 } \\ & = \sqrt{25 + 144 } \\ & = \sqrt{ 169 } \\ & = 13 \end{align} $
*). Keliling $\Delta$DEF
$ \begin{align} \text{Keliling } \Delta DEF & = DE + EF + FD \\ & = 14 + 13 + 21 \\ & = 48 \end{align} $
sehingga keliling $\Delta$DEF adalah 48 cm.
*). Menentukan luas $\Delta$DEF, alasnya DE = 14 dan tingginya FG = 12,
$ \begin{align} \text{Luas } \Delta DEF & = \frac{1}{2} \times DE \times FG \\ & = \frac{1}{2} \times 14 \times 12 \\ & = 7 \times 12 \\ & = 84 \end{align} $
Jadi, luas $\Delta$DEF adalah 84 cm$^2$.
2). Sebuah syal berbentuk segitiga sama kaki dengan panjang sisi yang sama 12 cm dan panjang sisi lainnya 30 cm. Jika tinggi syal tersebut 9 cm, tentukan
a). keliling syal;
b). luas syal.
Penyelesaian :
*). Gambar segitiganya untuk mewakili bentuk syalnya :
a). Keliling syal adalah keliling segitiga,
$ \begin{align} \text{Keliling } \Delta & = 12 + 12 + 30 \\ & = 54 \end{align} $
keliling syal adalah 54 cm.
b). Luas syal adalah luas segitiga,
$ \begin{align} \text{Luas } \Delta DEF & = \frac{1}{2} \times a \times t \\ & = \frac{1}{2} \times 30 \times 9 \\ & = 15 \times 9 \\ & = 135 \end{align} $
Jadi, luas syal adalah 135 cm$^2$.
3). Tentukan luas dua bangun datar berikut,
Penyelesaian :
*). Luas bangun datar gambar (a),
$ \begin{align} L_1 & = \frac{1}{2} \times 5 \times 8 \\ & = 20 \\ L_2 & = \frac{1}{2} \times 7 \times 6 \\ & = 21 \end{align} $
Luas bangun seluruhnya pada gambar (a),
Luas total $ = L_1 + L_2 = 20 + 21 = 41 \, $ dm$^2$ .
*). Luas bangun datar gambar (b),
$ \begin{align} L_1 & = L_{ABE} = \frac{1}{2} \times 13 \times 8 \\ & = 52 \\ L_2 & = L_{BDE} = \frac{1}{2} \times 5 \times 12 \\ & = 30 \\ L_3 & = L_{BCD} = \frac{1}{2} \times 3 \times 4 \\ & = 6 \end{align} $
Luas bangun seluruhnya pada gambar (b),
Luas total $ = L_1 + L_2 + L_3 = 52 + 30 + 6 = 88 \, $ cm$^2$ .
4). Diketahui luas sebuah segitiga adalah 165 cm$^2$ dan panjang alasnya 22 cm. Hitunglah tinggi segitiga.
Penyelesaian :
*). Diketahui : $ L = 165 \, $ dan $ a = 22 $.
*). Menentukan tinggi segitiga ($t$),
$ \begin{align} L & = 165 \\ \frac{1}{2} \times a \times t & = 165 \\ \frac{1}{2} \times 22 \times t & = 165 \\ 11 \times t & = 165 \\ t & = \frac{165}{11} = 15 \end{align} $
Jadi, tinggi segitiga adalah 15 cm.