Penerapan lain trigonometri adalah pada lingkaran dan segitiga. Kali ini kita akan membahas materi Lingkaran Dalam dan Lingkaran Luar Segitiga. Namun sebelumnya, sebaiknya kita baca dulu materi aturan sinus pada artikel "Penerapan Trigonometri pada Segitiga : Aturan Sinus, Aturan Cosinus, Luas Segitiga".
Pembuktian Rumus luas segitiga lingkaran dalam :
*). Perhatikan gambar berikut.
Titik O adalah titik pusat lingkaran dengan jari-jari $ r $.
*). Menentukan luas segitiga ABC
Mislakan : $ s = \frac{a+b+c}{2} $
Luas segitiga = $ \frac{1}{2} \times \, $ alas $ \times \, $ tinggi.
$ \begin{align} L \, ABC & = L \, BOC + L \, AOC + L \, AOB \\ L \, ABC & = \frac{1}{2} a.r + \frac{1}{2} b.r + \frac{1}{2} a.r \\ & = \frac{1}{2} (a+b+c)r \\ & = r. \frac{a+b+c}{2} \\ L \, ABC & = r. s \end{align} $
Jadi, terbukti luas segitiganya : $ L \, ABC = rs $.
Contoh :
< 1). Diketahui lingkaran dalam segitiga ABC dengan panjang sisi-sisi segitiganya berturut-turut 4, 6, 8 . Tentukan jari-jari lingkaran dalamnya?
Penyelesaian :
*). Menentukan nilai $ s \, $ dan luas segitiga.
$ s = \frac{a+b+c}{2} = \frac{4 + 6 + 8}{2} = 9 $
Luas segitiga ABC dengan Rumus Heron.
$ L = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{9.(9-5)(9-6)(9-8)} = \sqrt{9.4.3.1} = 6\sqrt{3} $
*). Menentukan jari-jari segitiga dalamnya :
$ r = \frac{\text{Luas ABC }}{s} = \frac{6\sqrt{3}}{9} = \frac{2}{3}\sqrt{3} $
Pembuktian rumus luas segitiga lingkaran luar :
*). Luas segitiga ABC berdasarkan aturan sinus dan sudut A
$ \begin{align} \text{Luas ABC } = \frac{1}{2}bc \sin A \end{align} $
*). Sudut keliling lingkaran (sudut C) menghadap diameter, sehingga besar sudutnya $ 90^\circ \, $ .
*). Menentukan nilai sin A :
$ \sin A = \frac{de}{mi} \rightarrow \sin A = \frac{BC}{BA} \rightarrow \sin A = \frac{a}{2r} $
*). Substitusi bentuk $ \sin A = \frac{a}{2r} \, $ ke luas segitiga
$ \begin{align} \text{Luas ABC } & = \frac{1}{2}bc \sin A \\ \text{Luas ABC } & = \frac{1}{2}bc . \frac{a}{2r} \\ \text{Luas ABC } & = \frac{abc}{4r} \end{align} $
Jadi terbukti rumus luas segitiga lingkaran luar.
Contoh :
2). Tentukan jari-jari lingkaran luar segitiga ABC yang memiliki sisi-sisi 5, 6, 9 ?
Penyelesaian :
*). Misalkan $ a = 5, \, b = 6, \, c = 9 $
*). Menentukan nilai $ s $
$ \begin{align} s = \frac{a+b+c}{2} = \frac{5+6+9}{2} = 10 \end{align} $
*). Menentukan luas segitiga ABC
$ \begin{align} \text{Luas ABC } & = \sqrt{s(s-a)(s-b)(s-c)} \\ & = \sqrt{10(10-5)(10-6)(10-9)} \\ & = \sqrt{10.5.4.1} \\ & = 10\sqrt{2} \end{align} $
*). Menentukan jari-jari lingkaran luar.
$ \begin{align} r & = \frac{abc}{4\times \text{Luas ABC }} \\ r & = \frac{5.6.9}{4\times 10\sqrt{2}} \\ r & = \frac{27}{4\sqrt{2}} \\ r & = \frac{27}{8} \sqrt{2} \end{align} $
Jadi, jari-jari lingkarannya adalah $ r = \frac{27}{8} \sqrt{2} $ .
3). Perhatikan gambar berikut!
Segitiga ABC memiliki panjang BC = 6, AB = 8, AC = 10 .
Tentukan perbandingan jari-jari lingkaran luar dan lingkaran dalam segitiga?
Penyelesaian :
*). Menentukan nilai $ s $
$ \begin{align} s = \frac{a+b+c}{2} = \frac{6+8+10}{2} = 12 \end{align} $
*). Menentukan luas segitiga ABC.
$ \begin{align} \text{Luas ABC } & = \sqrt{s(s-a)(s-b)(s-c)} \\ & = \sqrt{12(12-6)(12-8)(12-10)} \\ & = \sqrt{12.6.4.2} \\ & = 24 \end{align} $
*). Menentukan jari-jari lingkaran luar segitiga ($r_1$)
$ \begin{align} r & = \frac{abc}{4\times \text{Luas ABC }} \\ r_1 & = \frac{6.8.10}{4\times 24} \\ r_1 & = 5 \end{align} $
*). Menentukan jari-jari lingkaran dalam segitiga ($r_2$)
$ \begin{align} r & = \frac{\text{Luas ABC }}{s} \\ r_2 & = \frac{24}{12} \\ r_2 & = 2 \end{align} $
*). Menentukan perbandingan jari-jari lingkaran :
$ \begin{align} \frac{r_1}{r_2} = \frac{5}{2} \end{align} $
Jadi, perbandingan jari-jari lingkaran luar dan lingkaran dalam adalah 5 : 2.
Lingkaran Dalam Segitiga
Lingkaran dalam segitiga maksudnya ada sebuah lingkaran yang dilukis di dalam segitiga yang mana lingkaran menyinggung ketiga sisi segitiganya. Berikut ilustrasi gambarnya.
Dari gambar di atas, diperoleh luas segitiga ABC :
$ \begin{align} \text{Luas ABC } = r s \end{align} \, $ atau $ \, \begin{align} r = \frac{\text{Luas ABC }}{s} \end{align} $
dengan $ s = \frac{a+b+c}{2} $
$ \begin{align} \text{Luas ABC } = r s \end{align} \, $ atau $ \, \begin{align} r = \frac{\text{Luas ABC }}{s} \end{align} $
dengan $ s = \frac{a+b+c}{2} $
*). Perhatikan gambar berikut.
*). Menentukan luas segitiga ABC
Mislakan : $ s = \frac{a+b+c}{2} $
Luas segitiga = $ \frac{1}{2} \times \, $ alas $ \times \, $ tinggi.
$ \begin{align} L \, ABC & = L \, BOC + L \, AOC + L \, AOB \\ L \, ABC & = \frac{1}{2} a.r + \frac{1}{2} b.r + \frac{1}{2} a.r \\ & = \frac{1}{2} (a+b+c)r \\ & = r. \frac{a+b+c}{2} \\ L \, ABC & = r. s \end{align} $
Jadi, terbukti luas segitiganya : $ L \, ABC = rs $.
Contoh :
< 1). Diketahui lingkaran dalam segitiga ABC dengan panjang sisi-sisi segitiganya berturut-turut 4, 6, 8 . Tentukan jari-jari lingkaran dalamnya?
Penyelesaian :
*). Menentukan nilai $ s \, $ dan luas segitiga.
$ s = \frac{a+b+c}{2} = \frac{4 + 6 + 8}{2} = 9 $
Luas segitiga ABC dengan Rumus Heron.
$ L = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{9.(9-5)(9-6)(9-8)} = \sqrt{9.4.3.1} = 6\sqrt{3} $
*). Menentukan jari-jari segitiga dalamnya :
$ r = \frac{\text{Luas ABC }}{s} = \frac{6\sqrt{3}}{9} = \frac{2}{3}\sqrt{3} $
Lingkaran Luar Segitiga
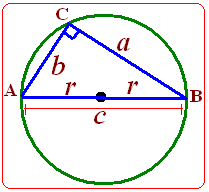
Perhatikan gambar lingkaran luar segitiga berikut.
Dari gambar, luas segitiga lingkaran luar segitiga adalah :
$ \begin{align} \text{Luas ABC } = \frac{abc}{4r} \end{align} \, $ atau $ \, \begin{align} r = \frac{abc}{4\times \text{Luas ABC }} \end{align} $
Dimana $ \begin{align} \text{Luas ABC } = \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
dengan $ \begin{align} s = \frac{a+b+c}{2} \end{align} $
$ \begin{align} \text{Luas ABC } = \frac{abc}{4r} \end{align} \, $ atau $ \, \begin{align} r = \frac{abc}{4\times \text{Luas ABC }} \end{align} $
Dimana $ \begin{align} \text{Luas ABC } = \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
dengan $ \begin{align} s = \frac{a+b+c}{2} \end{align} $
*). Luas segitiga ABC berdasarkan aturan sinus dan sudut A
$ \begin{align} \text{Luas ABC } = \frac{1}{2}bc \sin A \end{align} $
*). Sudut keliling lingkaran (sudut C) menghadap diameter, sehingga besar sudutnya $ 90^\circ \, $ .
*). Menentukan nilai sin A :
$ \sin A = \frac{de}{mi} \rightarrow \sin A = \frac{BC}{BA} \rightarrow \sin A = \frac{a}{2r} $
*). Substitusi bentuk $ \sin A = \frac{a}{2r} \, $ ke luas segitiga
$ \begin{align} \text{Luas ABC } & = \frac{1}{2}bc \sin A \\ \text{Luas ABC } & = \frac{1}{2}bc . \frac{a}{2r} \\ \text{Luas ABC } & = \frac{abc}{4r} \end{align} $
Jadi terbukti rumus luas segitiga lingkaran luar.
Contoh :
2). Tentukan jari-jari lingkaran luar segitiga ABC yang memiliki sisi-sisi 5, 6, 9 ?
Penyelesaian :
*). Misalkan $ a = 5, \, b = 6, \, c = 9 $
*). Menentukan nilai $ s $
$ \begin{align} s = \frac{a+b+c}{2} = \frac{5+6+9}{2} = 10 \end{align} $
*). Menentukan luas segitiga ABC
$ \begin{align} \text{Luas ABC } & = \sqrt{s(s-a)(s-b)(s-c)} \\ & = \sqrt{10(10-5)(10-6)(10-9)} \\ & = \sqrt{10.5.4.1} \\ & = 10\sqrt{2} \end{align} $
*). Menentukan jari-jari lingkaran luar.
$ \begin{align} r & = \frac{abc}{4\times \text{Luas ABC }} \\ r & = \frac{5.6.9}{4\times 10\sqrt{2}} \\ r & = \frac{27}{4\sqrt{2}} \\ r & = \frac{27}{8} \sqrt{2} \end{align} $
Jadi, jari-jari lingkarannya adalah $ r = \frac{27}{8} \sqrt{2} $ .
3). Perhatikan gambar berikut!
Tentukan perbandingan jari-jari lingkaran luar dan lingkaran dalam segitiga?
Penyelesaian :
*). Menentukan nilai $ s $
$ \begin{align} s = \frac{a+b+c}{2} = \frac{6+8+10}{2} = 12 \end{align} $
*). Menentukan luas segitiga ABC.
$ \begin{align} \text{Luas ABC } & = \sqrt{s(s-a)(s-b)(s-c)} \\ & = \sqrt{12(12-6)(12-8)(12-10)} \\ & = \sqrt{12.6.4.2} \\ & = 24 \end{align} $
*). Menentukan jari-jari lingkaran luar segitiga ($r_1$)
$ \begin{align} r & = \frac{abc}{4\times \text{Luas ABC }} \\ r_1 & = \frac{6.8.10}{4\times 24} \\ r_1 & = 5 \end{align} $
*). Menentukan jari-jari lingkaran dalam segitiga ($r_2$)
$ \begin{align} r & = \frac{\text{Luas ABC }}{s} \\ r_2 & = \frac{24}{12} \\ r_2 & = 2 \end{align} $
*). Menentukan perbandingan jari-jari lingkaran :
$ \begin{align} \frac{r_1}{r_2} = \frac{5}{2} \end{align} $
Jadi, perbandingan jari-jari lingkaran luar dan lingkaran dalam adalah 5 : 2.