Aplikasi turunan lain yang lebih menarik lagi adalah menggambar grafik fungsi, sehingga pada artikel kali ini kita akan membahas menggambar grafik fungsi menggunakan turunan baik fungsi aljabar maupun fungsi trigonometri. Untuk memudahkan mempelajari materi ini, sebaiknya kita pelajari dulu materi "turunan fungsi aljabar", "turunan fungsi trigonometri", serta "nilai stasionernya dan jenisnya".
Contoh :
1). Gambarlah grafik kurva $ y = 3x^2 - x^3 $.
Penyelesaian :
i). Menentukan titik potong pada sumbu-sumbu :
*). Tipot sumbu X, substitusi $ y = 0 $
$ \begin{align} y = 0 \rightarrow y & = 3x^2 - x^3 \\ 0 & = 3x^2 - x^3 \\ 3x^2 - x^3 & = 0 \\ x^2 ( 3 - x) & = 0 \\ x = 0 \vee x & = 3 \end{align} $
Sehingga titik potong sumbu X adalah (0,0) dan (3,0).
*). Tipot sumbu Y, substitusi $ x = 0 $
$ y = 3x^2 - x^3 = 3.0^2 - 0^3 = 0 $
Sehingga titik potong sumbu Y adalah (0,0).
ii). Menentukan titik-titik stasioner,
Fungsi : $ y = 3x^2 - x^3 $
$ f^\prime (x) = 6x - 3x^2 \, $ dan $ f^{\prime \prime } (x) = 6 - 6x $ .
*). Syarat stasioner : $ f^\prime (x) = 0 $
$ \begin{align} f^\prime (x) & = 0 \\ 6x - 3x^2 & = 0 \\ 3x ( 2 - x) & = 0 \\ x = 0 \vee x & = 2 \end{align} $
*). Nilai stasionernya : substitusi ke fungsi awal.
Untuk $ x = 0 \, $ , nilai stasionernya $ f(0) = 3.0^2 - 0^3 = 0 $
titik stasionernya (0,0) .
Untuk $ x = 2 \, $ , nilai stasionernya $ f(2) = 3.2^2 - 2^3 = 4 $
titik stasionernya (2,4).
*). Menentukan jenis stasionernya, gunakan turunan kedua : $ f^{\prime \prime } (x) = 6 - 6x $
Untuk $ x = 0 \rightarrow f^{\prime \prime } (0) = 6 - 6.0 = 6 \, $ (positif) , jenisnya minimum.
Untuk $ x = 2 \rightarrow f^{\prime \prime } (2) = 6 - 6.2 = -6 \, $ (negatif) , jenisnya maksimum.
Artinya titik (0,0) adalah titik balik minimum dan titik (2,4) adalah titik balik maksimum.
iii). Berdasarkan fungsi $ y = 3x^2 - x^3 , \, $ kita substitusi beberapa nilai $ x \, $ yaitu :
Untuk $ x \, $ semakin besar, nilai $ y \, $ semakin besar negatif (ke bawah) dan untuk $ x \, $ semakin kecil, nilai $ y \, $ semakin besar positif (ke atas).
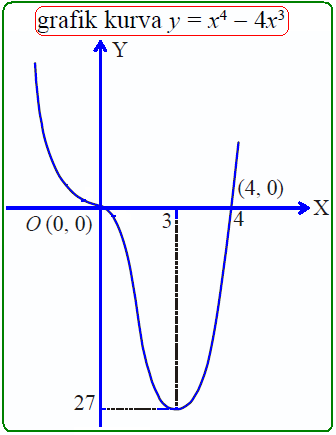
2). Gambarlah grafik kurva $ y = x^4 - 4x^3 $ .
Penyelesaian :
i). Menentukan titik potong pada sumbu-sumbu :
*). Tipot sumbu X, substitusi $ y = 0 $
$ \begin{align} y = 0 \rightarrow y & = x^4 - 4x^3 \\ 0 & = x^4 - 4x^3 \\ x^4 - 4x^3 & = 0 \\ x^3 ( x - 4 ) & = 0 \\ x = 0 \vee x & = 4 \end{align} $
Sehingga titik potong sumbu X adalah (0,0) dan (4,0).
*). Tipot sumbu Y, substitusi $ x = 0 $
$ y = x^4 - 4x^3 = 0^4 - 4.0^3 = 0 $
Sehingga titik potong sumbu Y adalah (0,0).
ii). Menentukan titik-titik stasioner,
Fungsi : $ y = x^4 - 4x^3 $
$ f^\prime (x) = 4x^3 - 12x^2 \, $ dan $ f^{\prime \prime } (x) = 12x^2 - 24x $ .
*). Syarat stasioner : $ f^\prime (x) = 0 $
$ \begin{align} f^\prime (x) & = 0 \\ 4x^3 - 12x^2 & = 0 \\ 4x^2 (x - 3) & = 0 \\ x = 0 \vee x & = 3 \end{align} $
*). Nilai stasionernya : substitusi ke fungsi awal.
Untuk $ x = 0 \, $ , nilai stasionernya $ f(0) = 0^4 - 4.0^3 = 0 $
titik stasionernya (0,0) .
Untuk $ x = 3 \, $ , nilai stasionernya $ f(2) = 3^4 - 4.3^3 = -27 $
titik stasionernya (3,-27).
*). Menentukan jenis stasionernya, gunakan turunan kedua : $ f^{\prime \prime } (x) = 12x^2 - 24x $
Untuk $ x = 0 \rightarrow f^{\prime \prime } (0) = 12.0^2 - 24.0 = 0 \, $ (nol) , jenisnya titik belok.
Untuk $ x = 3 \rightarrow f^{\prime \prime } (3) = 12.3^2 - 24.3 = 36 \, $ (positif) , jenisnya minimum.
Artinya titik (0,0) adalah titik belok dan titik (3,27) adalah titik balik minimum.
iii). Berdasarkan fungsi $ y = x^4 - 4x^3 , \, $ kita substitusi beberapa nilai $ x \, $ yaitu :
Untuk $ x \, $ semakin besar, nilai $ y \, $ semakin besar positif (ke atas) dan untuk $ x \, $ semakin kecil, nilai $ y \, $ semakin besar positif (ke atas).
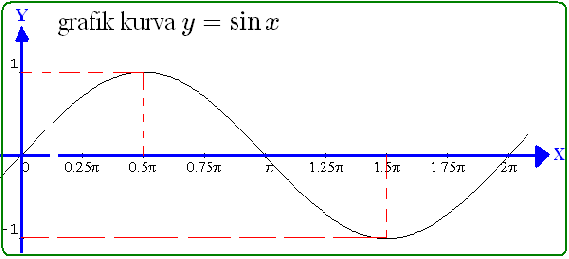
3). Gambarlah grafik kurva $ y = \sin x \, $ untuk $ 0 \leq x \leq 360^\circ $ .
Penyelesaian :
i). Menentukan titik potong pada sumbu-sumbu :
*). Tipot sumbu X, substitusi $ y = 0 $
$ \begin{align} y = 0 \rightarrow y & = \sin x \\ 0 & = \sin x \\ \sin x & = 0 \\ x = 0 , \, x = 180^\circ = \pi \vee x & = 360^\circ = 2\pi \end{align} $
Sehingga titik potong sumbu X adalah $ (0,0), \, (180^\circ , 0), \, (360^\circ, 0) $ .
*). Tipot sumbu Y, substitusi $ x = 0 $
$ y = \sin x = \sin 0 = 0 $
Sehingga titik potong sumbu Y adalah (0,0).
ii). Menentukan titik-titik stasioner,
Fungsi : $ y = \sin x $
$ f^\prime (x) = \cos x \, $ dan $ f^{\prime \prime } (x) = -\sin x $ .
*). Syarat stasioner : $ f^\prime (x) = 0 $
$ \begin{align} f^\prime (x) & = 0 \\ \cos x & = 0 \\ x = 90^\circ = \frac{1}{2}\pi \vee x & = 270^\circ = \frac{3}{2}\pi \end{align} $
*). Nilai stasionernya : substitusi ke fungsi awal.
Untuk $ x = 90^\circ \, $ , nilai stasionernya $ f(90^\circ) = \sin 90^\circ = 1 $
titik stasionernya ($ 90^\circ , 1$) .
Untuk $ x = 270^\circ \, $ , nilai stasionernya $ f(270^\circ) = \sin 270^\circ = -1 $
titik stasionernya ($ 270^\circ , -1$).
*). Menentukan jenis stasionernya, gunakan turunan kedua : $ f^{\prime \prime } (x) = -\sin x $
Untuk $ x = 90^\circ \rightarrow f^{\prime \prime } (90^\circ) = - \sin 90^\circ = -1 \, $ (negatif) , jenisnya maksimum.
Untuk $ x = 270^\circ \rightarrow f^{\prime \prime } (270^\circ) = -\sin 270^\circ = 1 \, $ (positif) , jenisnya minimum.
Artinya titik ($ 90^\circ , 1$) adalah titik balik maksimum dan titik ($ 270^\circ , -1$) adalah titik balik minimum.
Berikut gambar grafik fungsi $ y = \sin x \, $ pada interval $ 0 \leq x \leq 360^\circ $ .
Langkah - Langkah Menggambar Grafik Fungsi Menggunakan Turunan
Berikut langkah-langkah mengambar grafik suatu fungsi menggunakan turunan :
i). Menentukan titik potong (tipot) dengan sumbu-sumbu koordinat (sumbu X dan sumbu Y).
Titik potong sumbu X, substitusi $ y = 0 $ .
Titik potong sumbu Y, substitusi $ x = 0 $ .
ii). Menentukan titik-titik stasioner dan jenisnya (titik balik minimum, titik balik maksimum, dan titik belok).
iii). Menentukan titik bantuan lain agar grafiknya lebih mudah sketsa, atau bisa juga secara umum menentukan nilai $ y $ untuk $ x $ besar positif dan untuk $ x $ besar negatif.
i). Menentukan titik potong (tipot) dengan sumbu-sumbu koordinat (sumbu X dan sumbu Y).
Titik potong sumbu X, substitusi $ y = 0 $ .
Titik potong sumbu Y, substitusi $ x = 0 $ .
ii). Menentukan titik-titik stasioner dan jenisnya (titik balik minimum, titik balik maksimum, dan titik belok).
iii). Menentukan titik bantuan lain agar grafiknya lebih mudah sketsa, atau bisa juga secara umum menentukan nilai $ y $ untuk $ x $ besar positif dan untuk $ x $ besar negatif.
1). Gambarlah grafik kurva $ y = 3x^2 - x^3 $.
Penyelesaian :
i). Menentukan titik potong pada sumbu-sumbu :
*). Tipot sumbu X, substitusi $ y = 0 $
$ \begin{align} y = 0 \rightarrow y & = 3x^2 - x^3 \\ 0 & = 3x^2 - x^3 \\ 3x^2 - x^3 & = 0 \\ x^2 ( 3 - x) & = 0 \\ x = 0 \vee x & = 3 \end{align} $
Sehingga titik potong sumbu X adalah (0,0) dan (3,0).
*). Tipot sumbu Y, substitusi $ x = 0 $
$ y = 3x^2 - x^3 = 3.0^2 - 0^3 = 0 $
Sehingga titik potong sumbu Y adalah (0,0).
ii). Menentukan titik-titik stasioner,
Fungsi : $ y = 3x^2 - x^3 $
$ f^\prime (x) = 6x - 3x^2 \, $ dan $ f^{\prime \prime } (x) = 6 - 6x $ .
*). Syarat stasioner : $ f^\prime (x) = 0 $
$ \begin{align} f^\prime (x) & = 0 \\ 6x - 3x^2 & = 0 \\ 3x ( 2 - x) & = 0 \\ x = 0 \vee x & = 2 \end{align} $
*). Nilai stasionernya : substitusi ke fungsi awal.
Untuk $ x = 0 \, $ , nilai stasionernya $ f(0) = 3.0^2 - 0^3 = 0 $
titik stasionernya (0,0) .
Untuk $ x = 2 \, $ , nilai stasionernya $ f(2) = 3.2^2 - 2^3 = 4 $
titik stasionernya (2,4).
*). Menentukan jenis stasionernya, gunakan turunan kedua : $ f^{\prime \prime } (x) = 6 - 6x $
Untuk $ x = 0 \rightarrow f^{\prime \prime } (0) = 6 - 6.0 = 6 \, $ (positif) , jenisnya minimum.
Untuk $ x = 2 \rightarrow f^{\prime \prime } (2) = 6 - 6.2 = -6 \, $ (negatif) , jenisnya maksimum.
Artinya titik (0,0) adalah titik balik minimum dan titik (2,4) adalah titik balik maksimum.
iii). Berdasarkan fungsi $ y = 3x^2 - x^3 , \, $ kita substitusi beberapa nilai $ x \, $ yaitu :
Untuk $ x \, $ semakin besar, nilai $ y \, $ semakin besar negatif (ke bawah) dan untuk $ x \, $ semakin kecil, nilai $ y \, $ semakin besar positif (ke atas).
2). Gambarlah grafik kurva $ y = x^4 - 4x^3 $ .
Penyelesaian :
i). Menentukan titik potong pada sumbu-sumbu :
*). Tipot sumbu X, substitusi $ y = 0 $
$ \begin{align} y = 0 \rightarrow y & = x^4 - 4x^3 \\ 0 & = x^4 - 4x^3 \\ x^4 - 4x^3 & = 0 \\ x^3 ( x - 4 ) & = 0 \\ x = 0 \vee x & = 4 \end{align} $
Sehingga titik potong sumbu X adalah (0,0) dan (4,0).
*). Tipot sumbu Y, substitusi $ x = 0 $
$ y = x^4 - 4x^3 = 0^4 - 4.0^3 = 0 $
Sehingga titik potong sumbu Y adalah (0,0).
ii). Menentukan titik-titik stasioner,
Fungsi : $ y = x^4 - 4x^3 $
$ f^\prime (x) = 4x^3 - 12x^2 \, $ dan $ f^{\prime \prime } (x) = 12x^2 - 24x $ .
*). Syarat stasioner : $ f^\prime (x) = 0 $
$ \begin{align} f^\prime (x) & = 0 \\ 4x^3 - 12x^2 & = 0 \\ 4x^2 (x - 3) & = 0 \\ x = 0 \vee x & = 3 \end{align} $
*). Nilai stasionernya : substitusi ke fungsi awal.
Untuk $ x = 0 \, $ , nilai stasionernya $ f(0) = 0^4 - 4.0^3 = 0 $
titik stasionernya (0,0) .
Untuk $ x = 3 \, $ , nilai stasionernya $ f(2) = 3^4 - 4.3^3 = -27 $
titik stasionernya (3,-27).
*). Menentukan jenis stasionernya, gunakan turunan kedua : $ f^{\prime \prime } (x) = 12x^2 - 24x $
Untuk $ x = 0 \rightarrow f^{\prime \prime } (0) = 12.0^2 - 24.0 = 0 \, $ (nol) , jenisnya titik belok.
Untuk $ x = 3 \rightarrow f^{\prime \prime } (3) = 12.3^2 - 24.3 = 36 \, $ (positif) , jenisnya minimum.
Artinya titik (0,0) adalah titik belok dan titik (3,27) adalah titik balik minimum.
iii). Berdasarkan fungsi $ y = x^4 - 4x^3 , \, $ kita substitusi beberapa nilai $ x \, $ yaitu :
Untuk $ x \, $ semakin besar, nilai $ y \, $ semakin besar positif (ke atas) dan untuk $ x \, $ semakin kecil, nilai $ y \, $ semakin besar positif (ke atas).
3). Gambarlah grafik kurva $ y = \sin x \, $ untuk $ 0 \leq x \leq 360^\circ $ .
Penyelesaian :
i). Menentukan titik potong pada sumbu-sumbu :
*). Tipot sumbu X, substitusi $ y = 0 $
$ \begin{align} y = 0 \rightarrow y & = \sin x \\ 0 & = \sin x \\ \sin x & = 0 \\ x = 0 , \, x = 180^\circ = \pi \vee x & = 360^\circ = 2\pi \end{align} $
Sehingga titik potong sumbu X adalah $ (0,0), \, (180^\circ , 0), \, (360^\circ, 0) $ .
*). Tipot sumbu Y, substitusi $ x = 0 $
$ y = \sin x = \sin 0 = 0 $
Sehingga titik potong sumbu Y adalah (0,0).
ii). Menentukan titik-titik stasioner,
Fungsi : $ y = \sin x $
$ f^\prime (x) = \cos x \, $ dan $ f^{\prime \prime } (x) = -\sin x $ .
*). Syarat stasioner : $ f^\prime (x) = 0 $
$ \begin{align} f^\prime (x) & = 0 \\ \cos x & = 0 \\ x = 90^\circ = \frac{1}{2}\pi \vee x & = 270^\circ = \frac{3}{2}\pi \end{align} $
*). Nilai stasionernya : substitusi ke fungsi awal.
Untuk $ x = 90^\circ \, $ , nilai stasionernya $ f(90^\circ) = \sin 90^\circ = 1 $
titik stasionernya ($ 90^\circ , 1$) .
Untuk $ x = 270^\circ \, $ , nilai stasionernya $ f(270^\circ) = \sin 270^\circ = -1 $
titik stasionernya ($ 270^\circ , -1$).
*). Menentukan jenis stasionernya, gunakan turunan kedua : $ f^{\prime \prime } (x) = -\sin x $
Untuk $ x = 90^\circ \rightarrow f^{\prime \prime } (90^\circ) = - \sin 90^\circ = -1 \, $ (negatif) , jenisnya maksimum.
Untuk $ x = 270^\circ \rightarrow f^{\prime \prime } (270^\circ) = -\sin 270^\circ = 1 \, $ (positif) , jenisnya minimum.
Artinya titik ($ 90^\circ , 1$) adalah titik balik maksimum dan titik ($ 270^\circ , -1$) adalah titik balik minimum.
Berikut gambar grafik fungsi $ y = \sin x \, $ pada interval $ 0 \leq x \leq 360^\circ $ .