Setelah kita mempelajari beberapa materi prasayarat untuk program linear seperti : "Persamaan dan Grafik Bentuk Linear", "Menentukan Daerah Penyelesaian (Arsiran) sistem Pertidaksamaan", dan "Menyusun Model Matematika", maka tiba saatnya kita akan membahas masalah program linear yang langsung berkaitan dengan nilai optimum yaitu nilai maksimum atau nilai minimum pada artikel Program Linear : Nilai Optimum dengan Uji Titik Pojok.
Untuk menentukan nilai optimum suatu soal cerita yang berkaitan dengan progrma linear, ada tiga metode yang bisa kita gunakan yaitu metode uji titik pojok, metode garis selidik, dan metode gradien. Namun diatara ketiga metode tersebut, yang paling mudah dan yang paling sering diajarkan adalah metode yang pertama yaitu metode uji titik pojok.
Contoh soal nilai optimum dengan uji titik pojok :
1). Tentukan nilai maksimum fungsi tujuan $ f(x,y) = 1.500x + 1.250y \, $ berdasarkan DHP berikut ini.
Penyelesaian :
*). Titik pojoknya adalah titik A, B, C, dan O. Titik C belum ada koordinatnya, sehingga harus kita cari dulu dengan eliminasi kedua persamaan garis.
*). Menentukan titik C :
$ \begin{array}{c|c|cc} x + y = 60 & \times 2.000 & 2.000x + 2.000y = 120.000 & \\ 2.500x + 2.000y = 140.000 & \times 1 & 2.500x + 2.000y = 140.000 & - \\ \hline & & -500x = -20.000 & \\ & & x = 40 & \end{array} $
Substitusi $ x = 40 \, $ ke persamaan $ x + y = 60 $
$ x + y = 60 \rightarrow 40 + y = 60 \rightarrow y = 20 $.
Sehingga titik C adalah C(40,20).
*). Substitusi semua titik pojok ke fungsi tujuan : $ f(x,y) = 1.500x + 1.250y $.
$ A(0,60) \rightarrow f = 1.500 \times 0 + 1.250 \times 60 = 75.000 $
$ B(56,0) \rightarrow f = 1.500 \times 56 + 1.250 \times 0 = 84.000 $
$ C(40,20) \rightarrow f = 1.500 \times 40 + 1.250 \times 20 = 85.000 $
$ O(0,0) \rightarrow f = 1.500 \times 0 + 1.250 \times 0 = 0 $
Jadi, fungsi $ f(x,y) = 1.500x + 1.250y \, $ di titik C(40,20) dengan nilai maksimumnya adalah $ f = 85.000 $.
2). Tentukan nilai maksimum $ f(x, y) = 3x + 4y \, $ pada himpunan penyelesaian sistem pertidaksamaan berikut.
$ x + 2y \leq 10, \, 4x + 3y \leq 24, \, x \geq 0, \, y \geq 0 $.
Penyelesaian :
*). Pada soal ini model matematikanya sudah ada, sehingga kita lanjutkan dengan menentukan DHP dengan menggambar grafiknya dan menentukan titik pojoknya.
*). Menggambar grafik dan DHP.
Silahkan baca : "Persamaan dan Grafik Bentuk Linear", dan "Menentukan DHP sistem Pertidaksamaan".
$ x + 2y = 10 \rightarrow (0,5), (10,0) $
$ 4x + 3y = 24 \rightarrow (0,8), (6,0) $
grafik dan DHP nya :
*). Titik pojoknya adalah titik O, A, B, dan C.
Titik B belum ada koordinatnya, sehingga kita cari dulu dengan eliminasi kedua persamaannya :
$ \begin{array}{c|c|cc} x + 2y = 10 & \times 4 & 4x + 8y = 40 & \\ 4x + 3y = 24 & \times 1 & 4x + 3y = 24 & - \\ \hline & & 5y = 16 & \\ & & y = \frac{16}{5} & \end{array} $
Substitusi $ y = \frac{16}{5} \, $ ke persamaan $ x + 2y = 10 $
$ x + 2y = 10 \rightarrow x + 2\times \left( \frac{16}{5} \right) = 10 \rightarrow x = \frac{18}{5} $.
Sehingga titik B adalah B($\frac{18}{5},\frac{16}{5}$).
*). Substitusi semua titik pojok ke fungsi tujuannya : $ f(x,y) = 3x + 4y \, $ dan hasilnya seperti tabel berikut ini,
Tabel nilai fungsi tujuannya :
Jadi, nilai minimum fungsi $ f(x,y) = 3x + 4y \, $ adalah 23,6.
3). Seorang anak penderita kekurangan gizi diharuskan makan dua jenis tablet vitamin setiap hari. Tablet pertama mengandung 5 unit vitamin A dan 3 unit vitamin B, sedangkan tablet kedua mengandung 10 unit vitamin A dan 1 unit vitamin B. Dalam satu hari, anak itu memerlukan 20 unit vitamin A dan 5 unit vitamin B. Jika harga tablet pertama Rp400,00/biji dan tablet kedua Rp600,00/biji, tentukan pengeluaran minimum untuk pembelian tablet per harinya.
Penyelesaian :
*). Pertama kita buat model matematikanya dulu :
Silahkan baca : "Menyusun Model Matematika".
Misalkan, banyaknya tablet 1 sebanyak $ x $ biji dan tablet 2 sebanyak $ y $ biji.
Tabel untuk membuat model matematika,
Kebutuhan vitamin yang optimal adalah tidak boleh kurang dari, sehingga tanda ketaksamaan yang digunakan adalah "$\geq$".
Model matematikanya :
Kendalanya : $ 5x + 10y \geq 20 , \, 3x + y \geq 5 , \, x \geq 0, \, y \geq 0 $.
Fungsi Tujuannya : $ z = f(x,y) = 400x + 600y $.
*). Menentukan Grafik dan DHP nya :
$ 5x + 10y \geq 20 \rightarrow (0,2),(4,0) $
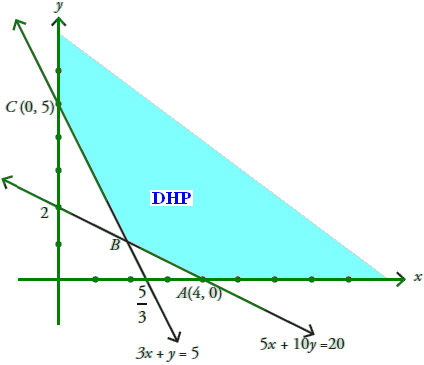
$ 3x + y \geq 5 \rightarrow (0,5),(\frac{5}{3},0) $
grafik dan DHP nya :
*). Titik Pojoknya adalah titik A, B, dan C.
Kita tentukan koordinat titik B dengan eliminasi kedua persamaan :
$ \begin{array}{c|c|cc} 5x + 10y = 20 & \times 1 & 5x + 10y = 20 & \\ 3x + y = 5 & \times 10 & 30x + 10y = 50 & - \\ \hline & & -25x = -30 & \\ & & x = \frac{6}{5} & \end{array} $
Substitusi $ x = \frac{6}{5} \, $ ke persamaan $ 3x + y = 5 $
$ 3x + y = 5 \rightarrow 3x \times \frac{6}{5} + y = 5 \rightarrow y = \frac{7}{5} $.
Sehingga titik B adalah B($\frac{6}{5},\frac{7}{5}$).
*). Substitusi semua titik pojok ke fungsi tujuannya : $ z = f(x,y) = 400x + 600y \, $ dan hasilnya seperti tabel berikut ini,
Tabel nilai fungsi tujuannya :
Jadi, nilai minimum untuk fungsi tujuan tersebut adalah 1.320. Artinya, pengeluaran minimum untuk pembelian tablet per harinya Rp1.320,00.
4). Sebuah perusahaan memproduksi sepeda dan skuter dengan menggunakan dua mesin. Untuk memproduksi sepeda dibutuhkan waktu 5 jam dengan menggunakan mesin pertama dan 2 jam dengan menggunakan mesin kedua. Untuk memproduksi skuter dibutuhkan waktu 3 jam dengan menggunakan mesin pertama dan 6 jam dengan menggunakan mesin kedua. Kapasitas maksimum mesin pertama 150 jam, sedangkan kapasitas maksimum mesin kedua 180 jam. Keuntungan bersih yang diperoleh dari tiap satu unit sepeda adalah Rp480.000,00 dan satu unit skuter adalah Rp560.000,00. Tentukan jumlah sepeda dan skuter yang harus diproduksi agar diperoleh keuntungan maksimum!
Penyelesaian :
*). Langkah pertama adalah membuat model matematika dari masalah di atas. Misalkan banyaknya sepeda dinyatakan dengan $ x $ dan banyaknya skuter dinyatakan dengan $ y $.
Tabel model matematikanya :
Model matematikanya :
Kendala : $ 5x + 3y \leq 150, \, 2x + 6y \leq 180, \, x \geq 0 , \, y \geq 0 $ .
Fungsi tujuan : $ z = f(x,y) = 480.000x + 560.000y $ .
*). Menentukan Grafik dan DHP nya :
$ 5x + 3y = 150 \rightarrow (0,50),(30,0) $
$ 2x + 6y = 180 \rightarrow (0,30),(90,0) $
grafik dan DHP nya :
*). Titik Pojoknya adalah titik A, B, dan C.
Kita tentukan koordinat titik B dengan eliminasi kedua persamaan :
Sehingga titik B adalah B(15,25).
*). Substitusi semua titik pojok ke fungsi tujuannya : $ z = f(x,y) = 480.000x + 560.000y \, $ dan hasilnya seperti tabel berikut ini,
Tabel nilai fungsi tujuannya :
Jadi, nilai maksimum dari $ f(x,y) = 480.000x + 560.000y \, $ adalah 21.200.000.
Untuk menentukan nilai optimum suatu soal cerita yang berkaitan dengan progrma linear, ada tiga metode yang bisa kita gunakan yaitu metode uji titik pojok, metode garis selidik, dan metode gradien. Namun diatara ketiga metode tersebut, yang paling mudah dan yang paling sering diajarkan adalah metode yang pertama yaitu metode uji titik pojok.
Nilai Optimum dengan Uji Titik Pojok
Metode Uji titik pojok adalah suatu metode dengan mensubstitusikan titik-titik pojok pada suatu daerah himpunan penyelesaian (DHP) ke fungsi tujuannya (fungsi sasaran/fungsi objektif). Nilai maksimum berarti nilai yang paling besar yang kita ambil, begitu juga sebaliknya untuk nilai minimum kita ambil yang paling kecil.
Dari gambar DHP di atas, titik pojoknya adalah titik A, titik B, dan titik C.
Langkah-langkah menentukan nilai Optimum dengan uji titik pojok :
i). Buat model matematikanya (terdiri dari fungsi kendala dan fungsi tujuan).
ii). Tentukan daerah himpunan penyelesaiannya (DHP) dan titik pojoknya.
iii). Substitusi semua titik pojok ke fungsi tujuannya, dan tentukan yang diminta apakah nilai maksimum atau nilai minimum.
Langkah-langkah menentukan nilai Optimum dengan uji titik pojok :
i). Buat model matematikanya (terdiri dari fungsi kendala dan fungsi tujuan).
ii). Tentukan daerah himpunan penyelesaiannya (DHP) dan titik pojoknya.
iii). Substitusi semua titik pojok ke fungsi tujuannya, dan tentukan yang diminta apakah nilai maksimum atau nilai minimum.
1). Tentukan nilai maksimum fungsi tujuan $ f(x,y) = 1.500x + 1.250y \, $ berdasarkan DHP berikut ini.
*). Titik pojoknya adalah titik A, B, C, dan O. Titik C belum ada koordinatnya, sehingga harus kita cari dulu dengan eliminasi kedua persamaan garis.
*). Menentukan titik C :
$ \begin{array}{c|c|cc} x + y = 60 & \times 2.000 & 2.000x + 2.000y = 120.000 & \\ 2.500x + 2.000y = 140.000 & \times 1 & 2.500x + 2.000y = 140.000 & - \\ \hline & & -500x = -20.000 & \\ & & x = 40 & \end{array} $
Substitusi $ x = 40 \, $ ke persamaan $ x + y = 60 $
$ x + y = 60 \rightarrow 40 + y = 60 \rightarrow y = 20 $.
Sehingga titik C adalah C(40,20).
*). Substitusi semua titik pojok ke fungsi tujuan : $ f(x,y) = 1.500x + 1.250y $.
$ A(0,60) \rightarrow f = 1.500 \times 0 + 1.250 \times 60 = 75.000 $
$ B(56,0) \rightarrow f = 1.500 \times 56 + 1.250 \times 0 = 84.000 $
$ C(40,20) \rightarrow f = 1.500 \times 40 + 1.250 \times 20 = 85.000 $
$ O(0,0) \rightarrow f = 1.500 \times 0 + 1.250 \times 0 = 0 $
Jadi, fungsi $ f(x,y) = 1.500x + 1.250y \, $ di titik C(40,20) dengan nilai maksimumnya adalah $ f = 85.000 $.
2). Tentukan nilai maksimum $ f(x, y) = 3x + 4y \, $ pada himpunan penyelesaian sistem pertidaksamaan berikut.
$ x + 2y \leq 10, \, 4x + 3y \leq 24, \, x \geq 0, \, y \geq 0 $.
Penyelesaian :
*). Pada soal ini model matematikanya sudah ada, sehingga kita lanjutkan dengan menentukan DHP dengan menggambar grafiknya dan menentukan titik pojoknya.
*). Menggambar grafik dan DHP.
Silahkan baca : "Persamaan dan Grafik Bentuk Linear", dan "Menentukan DHP sistem Pertidaksamaan".
$ x + 2y = 10 \rightarrow (0,5), (10,0) $
$ 4x + 3y = 24 \rightarrow (0,8), (6,0) $
grafik dan DHP nya :
Titik B belum ada koordinatnya, sehingga kita cari dulu dengan eliminasi kedua persamaannya :
$ \begin{array}{c|c|cc} x + 2y = 10 & \times 4 & 4x + 8y = 40 & \\ 4x + 3y = 24 & \times 1 & 4x + 3y = 24 & - \\ \hline & & 5y = 16 & \\ & & y = \frac{16}{5} & \end{array} $
Substitusi $ y = \frac{16}{5} \, $ ke persamaan $ x + 2y = 10 $
$ x + 2y = 10 \rightarrow x + 2\times \left( \frac{16}{5} \right) = 10 \rightarrow x = \frac{18}{5} $.
Sehingga titik B adalah B($\frac{18}{5},\frac{16}{5}$).
*). Substitusi semua titik pojok ke fungsi tujuannya : $ f(x,y) = 3x + 4y \, $ dan hasilnya seperti tabel berikut ini,
Tabel nilai fungsi tujuannya :
3). Seorang anak penderita kekurangan gizi diharuskan makan dua jenis tablet vitamin setiap hari. Tablet pertama mengandung 5 unit vitamin A dan 3 unit vitamin B, sedangkan tablet kedua mengandung 10 unit vitamin A dan 1 unit vitamin B. Dalam satu hari, anak itu memerlukan 20 unit vitamin A dan 5 unit vitamin B. Jika harga tablet pertama Rp400,00/biji dan tablet kedua Rp600,00/biji, tentukan pengeluaran minimum untuk pembelian tablet per harinya.
Penyelesaian :
*). Pertama kita buat model matematikanya dulu :
Silahkan baca : "Menyusun Model Matematika".
Misalkan, banyaknya tablet 1 sebanyak $ x $ biji dan tablet 2 sebanyak $ y $ biji.
Tabel untuk membuat model matematika,
Model matematikanya :
Kendalanya : $ 5x + 10y \geq 20 , \, 3x + y \geq 5 , \, x \geq 0, \, y \geq 0 $.
Fungsi Tujuannya : $ z = f(x,y) = 400x + 600y $.
*). Menentukan Grafik dan DHP nya :
$ 5x + 10y \geq 20 \rightarrow (0,2),(4,0) $
$ 3x + y \geq 5 \rightarrow (0,5),(\frac{5}{3},0) $
grafik dan DHP nya :
Kita tentukan koordinat titik B dengan eliminasi kedua persamaan :
$ \begin{array}{c|c|cc} 5x + 10y = 20 & \times 1 & 5x + 10y = 20 & \\ 3x + y = 5 & \times 10 & 30x + 10y = 50 & - \\ \hline & & -25x = -30 & \\ & & x = \frac{6}{5} & \end{array} $
Substitusi $ x = \frac{6}{5} \, $ ke persamaan $ 3x + y = 5 $
$ 3x + y = 5 \rightarrow 3x \times \frac{6}{5} + y = 5 \rightarrow y = \frac{7}{5} $.
Sehingga titik B adalah B($\frac{6}{5},\frac{7}{5}$).
*). Substitusi semua titik pojok ke fungsi tujuannya : $ z = f(x,y) = 400x + 600y \, $ dan hasilnya seperti tabel berikut ini,
Tabel nilai fungsi tujuannya :
4). Sebuah perusahaan memproduksi sepeda dan skuter dengan menggunakan dua mesin. Untuk memproduksi sepeda dibutuhkan waktu 5 jam dengan menggunakan mesin pertama dan 2 jam dengan menggunakan mesin kedua. Untuk memproduksi skuter dibutuhkan waktu 3 jam dengan menggunakan mesin pertama dan 6 jam dengan menggunakan mesin kedua. Kapasitas maksimum mesin pertama 150 jam, sedangkan kapasitas maksimum mesin kedua 180 jam. Keuntungan bersih yang diperoleh dari tiap satu unit sepeda adalah Rp480.000,00 dan satu unit skuter adalah Rp560.000,00. Tentukan jumlah sepeda dan skuter yang harus diproduksi agar diperoleh keuntungan maksimum!
Penyelesaian :
*). Langkah pertama adalah membuat model matematika dari masalah di atas. Misalkan banyaknya sepeda dinyatakan dengan $ x $ dan banyaknya skuter dinyatakan dengan $ y $.
Tabel model matematikanya :
Kendala : $ 5x + 3y \leq 150, \, 2x + 6y \leq 180, \, x \geq 0 , \, y \geq 0 $ .
Fungsi tujuan : $ z = f(x,y) = 480.000x + 560.000y $ .
*). Menentukan Grafik dan DHP nya :
$ 5x + 3y = 150 \rightarrow (0,50),(30,0) $
$ 2x + 6y = 180 \rightarrow (0,30),(90,0) $
grafik dan DHP nya :
Kita tentukan koordinat titik B dengan eliminasi kedua persamaan :
Sehingga titik B adalah B(15,25).
*). Substitusi semua titik pojok ke fungsi tujuannya : $ z = f(x,y) = 480.000x + 560.000y \, $ dan hasilnya seperti tabel berikut ini,
Tabel nilai fungsi tujuannya :