Soal-soal pada Soal dan Pembahasan Garis dan Sudut yang menarik untuk dikerjakan tentu soal nomor 3. Butuh kiat-kiat khusus untuk menyelesaikannya, semisal dengan memperpanjang salah satu garis agar terbentuk suatu hubungan antara garis-garis dan sudut yang terbentuk. Tetap harus berusaha terlebih dahulu, kalau ada yang sulit sekali baru kita lihat pembahasannya yang ada pada artikel ini.
Soal 1.
Jika sudut m$\angle $ A $ = \frac{1}{8} \, $ putaran penuh, maka tentukanlah sudut:
a. Besar sudut penyiku $\angle $A.
b. Besar sudut pelurus $\angle $A.
a. Besar sudut penyiku $\angle $A.
b. Besar sudut pelurus $\angle $A.
Penyelesaian :
*). Menentukan besar sudut A :
$ \angle A = \frac{1}{8} \, $ putaran penuh $ = \frac{1}{8} . 360^\circ = 45^\circ $
a. Besar sudut penyiku $\angle $A $ = 90^\circ - 45^\circ = 45^\circ $ .
b. Besar sudut pelurus $\angle $A $ = 180^\circ - 45^\circ = 135^\circ $ .
*). Menentukan besar sudut A :
$ \angle A = \frac{1}{8} \, $ putaran penuh $ = \frac{1}{8} . 360^\circ = 45^\circ $
a. Besar sudut penyiku $\angle $A $ = 90^\circ - 45^\circ = 45^\circ $ .
b. Besar sudut pelurus $\angle $A $ = 180^\circ - 45^\circ = 135^\circ $ .
Soal 2.
Perhatikanlah gambar berikut ini.
Tentukan sudut-sudut yang merupakan pasangan sudut luar berseberangan dengan sudut-sudut berikut.
a. $\angle $FID
b. $\angle $JKB
c. $\angle $CIE
a. $\angle $FID
b. $\angle $JKB
c. $\angle $CIE
Penyelesaian :
*). Sudut FID dan sudut JKB adalah sudut dalam pada garis sejajar AB dan CD sehingga sudut FID dan JKB tidak memiliki pasangan sudut luar bersebrangan, ini sekaligus menjawab pertanyaan a dan b.
c). Sudut CIE luar bersebrangan dengan sudut FKB.
*). Sudut FID dan sudut JKB adalah sudut dalam pada garis sejajar AB dan CD sehingga sudut FID dan JKB tidak memiliki pasangan sudut luar bersebrangan, ini sekaligus menjawab pertanyaan a dan b.
c). Sudut CIE luar bersebrangan dengan sudut FKB.
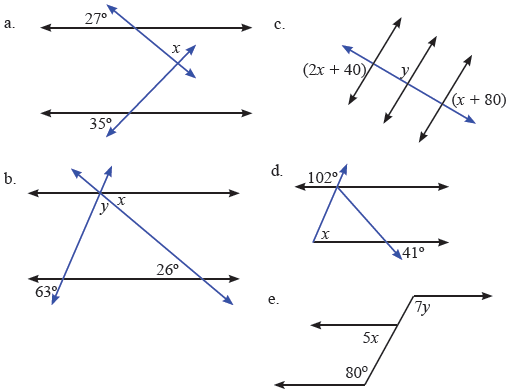
Soal 3.
Tentukan nilai x dan y pada gambar berikut.
Penyelesaian :
*). Untuk mempermudah penyelesaiannya, perlu beberapa gambar kita tambahkan garis sehingga akan membantu kita.
a). Perhatikan gambar a berikut,
*). Sudut $ b \, $ dan $ 27^\circ \, $ adalah bertolak belakang, sehingga besarnya sama yaitu $ b = 27^\circ $
*). Sudut $ c \, $ dan $ 35^\circ \, $ adalah sehadap, sehingga besarnya sama yaitu $ c = 35^\circ $
*). Sudut $ b, \, c, \, $ dan $ \, x \, $ adalah sudut pada segitiga, jumlah sudut-sudut segitiga $ 180^\circ $
$ \begin{align} b + c + x & = 180^\circ \\ 27^\circ + 35^\circ + x & = 180^\circ \\ 62^\circ + x & = 180^\circ \\ x & = 180^\circ - 62^\circ \\ x & = 118^\circ \end{align} $
Jadi, nilai $ x = 118^\circ $ .
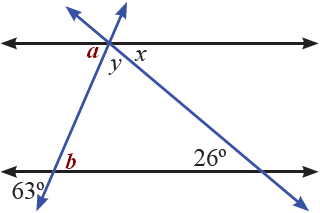
b). Perhatikan gambar b berikut,
*). Sudut $ x \, $ dan $ 26^\circ \, $ adalah dalam bersebrangan, sehingga besarnya sama yaitu $ x = 26^\circ $ .
*). Ada dua cara untuk menentukan nilai $ y $ :
Cara I : Berpelurus,
Sudut $ a \, $ sehadap dengan $ 63^\circ \, $ sehingga besarnya sama, $ a = 63^\circ $
Sudut $ a, \, y, \, x \, $ berpelurus, sehingga jumlahnya $ 180^\circ $ .
$ \begin{align} a + y + x & = 180^\circ \\ 63^\circ + y + 26^\circ & = 180^\circ \\ y + 89^\circ & = 180^\circ \\ y & = 180^\circ - 89^\circ \\ y & = 91^\circ \end{align} $
Jadi, nilai $ y = 91^\circ $
Cara II : Jumlah sudut segitiga $ = 180^\circ $
Sudut $ b \, $ bertolak belakang dengan $ 63^\circ \, $ sehingga besar sudutnya sama, $ b = 63^\circ $
Sudut $ b, \, y, \, x \, $ adalah sudut-sudut segitiga, sehingga jumlahnya $ 180^\circ $ .
$ \begin{align} b + y + x & = 180^\circ \\ 63^\circ + y + 26^\circ & = 180^\circ \\ y + 89^\circ & = 180^\circ \\ y & = 180^\circ - 89^\circ \\ y & = 91^\circ \end{align} $
Jadi, nilai $ y = 91^\circ $
Jadi, kesimulannya nilai $ x = 26^\circ \, $ dan $ y = 91^\circ $ .
c). Perhatikan gambar c berikut,
*). Sudut $ (2x+40) , \, m, \, n \, $ adalah sehadap sehingga besarnya sama, yaitu $ m = n = 2x + 40 $ .
*). Sudut $ n \, $ bertolak belakang dengan $ (x + 80) \, $ , sehingga besarnya sama,
$ \begin{align} n & = x + 80 \\ 2x + 40 & = x + 80 \\ x & = 40 \end{align} $
Sehingga nilai $ x = 40^\circ $
*). Sudut $ m \, $ dan $ y \, $ berpelurus, jumlahnya $ 180^\circ $
$ \begin{align} m + y & = 180^\circ \\ (2x + 40) + y & = 180^\circ \\ (2.40 + 40) + y & = 180^\circ \\ (80 + 40) + y & = 180^\circ \\ 120^\circ + y & = 180^\circ \\ y & = 180^\circ - 120^\circ \\ y & = 60^\circ \end{align} $
Jadi, nilai $ x = 40^\circ \, $ dan $ y = 60^\circ $ .
d). Perhatikan gambar d berikut,
*). Sudut $ a \, $ dan $ 102^\circ $ adalah sehadap, sehingga besarnya sama, $ a = 102^\circ $ .
*). Sudut $ a \, $ dan $ x \, $ berpelurus, jumlahnya $ 180^\circ $
$ \begin{align} a + x & = 180^\circ \\ 102^\circ + x & = 180^\circ \\ x & = 180^\circ - 102^\circ \\ x & = 78^\circ \end{align} $
Jadi, nilai $ x = 78^\circ $ .
e). Perhatikan gambar e berikut,
*). Sudut $ a \, $ dan $ 80^\circ \, $ bertolak belakang, sehingga besarnya sama, $ a = 80^\circ $
*). Sudut $ a \, $ dan $ 7y \, $ sehadap, sehingga besarnya sama,
$ 7y = 80^\circ \rightarrow y = \frac{80^\circ }{7} = 11\frac{3}{7} ^\circ $
*). Sudut $ 5x \, $ dan $ 80^\circ \, $ dalam sepihak, sehingga jumlahnya $ 180^\circ $
$ \begin{align} 5x + 80 & = 180^\circ \\ 5x & = 180^\circ - 80^\circ \\ 5x & = 100^\circ \\ x & = 20^\circ \end{align} $
Jadi, nilai $ x = 20^\circ \, $ dan $ y = 11\frac{3}{7} ^\circ $ .
*). Untuk mempermudah penyelesaiannya, perlu beberapa gambar kita tambahkan garis sehingga akan membantu kita.
a). Perhatikan gambar a berikut,
*). Sudut $ c \, $ dan $ 35^\circ \, $ adalah sehadap, sehingga besarnya sama yaitu $ c = 35^\circ $
*). Sudut $ b, \, c, \, $ dan $ \, x \, $ adalah sudut pada segitiga, jumlah sudut-sudut segitiga $ 180^\circ $
$ \begin{align} b + c + x & = 180^\circ \\ 27^\circ + 35^\circ + x & = 180^\circ \\ 62^\circ + x & = 180^\circ \\ x & = 180^\circ - 62^\circ \\ x & = 118^\circ \end{align} $
Jadi, nilai $ x = 118^\circ $ .
b). Perhatikan gambar b berikut,
*). Ada dua cara untuk menentukan nilai $ y $ :
Cara I : Berpelurus,
Sudut $ a \, $ sehadap dengan $ 63^\circ \, $ sehingga besarnya sama, $ a = 63^\circ $
Sudut $ a, \, y, \, x \, $ berpelurus, sehingga jumlahnya $ 180^\circ $ .
$ \begin{align} a + y + x & = 180^\circ \\ 63^\circ + y + 26^\circ & = 180^\circ \\ y + 89^\circ & = 180^\circ \\ y & = 180^\circ - 89^\circ \\ y & = 91^\circ \end{align} $
Jadi, nilai $ y = 91^\circ $
Cara II : Jumlah sudut segitiga $ = 180^\circ $
Sudut $ b \, $ bertolak belakang dengan $ 63^\circ \, $ sehingga besar sudutnya sama, $ b = 63^\circ $
Sudut $ b, \, y, \, x \, $ adalah sudut-sudut segitiga, sehingga jumlahnya $ 180^\circ $ .
$ \begin{align} b + y + x & = 180^\circ \\ 63^\circ + y + 26^\circ & = 180^\circ \\ y + 89^\circ & = 180^\circ \\ y & = 180^\circ - 89^\circ \\ y & = 91^\circ \end{align} $
Jadi, nilai $ y = 91^\circ $
Jadi, kesimulannya nilai $ x = 26^\circ \, $ dan $ y = 91^\circ $ .
c). Perhatikan gambar c berikut,
*). Sudut $ n \, $ bertolak belakang dengan $ (x + 80) \, $ , sehingga besarnya sama,
$ \begin{align} n & = x + 80 \\ 2x + 40 & = x + 80 \\ x & = 40 \end{align} $
Sehingga nilai $ x = 40^\circ $
*). Sudut $ m \, $ dan $ y \, $ berpelurus, jumlahnya $ 180^\circ $
$ \begin{align} m + y & = 180^\circ \\ (2x + 40) + y & = 180^\circ \\ (2.40 + 40) + y & = 180^\circ \\ (80 + 40) + y & = 180^\circ \\ 120^\circ + y & = 180^\circ \\ y & = 180^\circ - 120^\circ \\ y & = 60^\circ \end{align} $
Jadi, nilai $ x = 40^\circ \, $ dan $ y = 60^\circ $ .
d). Perhatikan gambar d berikut,
*). Sudut $ a \, $ dan $ x \, $ berpelurus, jumlahnya $ 180^\circ $
$ \begin{align} a + x & = 180^\circ \\ 102^\circ + x & = 180^\circ \\ x & = 180^\circ - 102^\circ \\ x & = 78^\circ \end{align} $
Jadi, nilai $ x = 78^\circ $ .
e). Perhatikan gambar e berikut,
*). Sudut $ a \, $ dan $ 7y \, $ sehadap, sehingga besarnya sama,
$ 7y = 80^\circ \rightarrow y = \frac{80^\circ }{7} = 11\frac{3}{7} ^\circ $
*). Sudut $ 5x \, $ dan $ 80^\circ \, $ dalam sepihak, sehingga jumlahnya $ 180^\circ $
$ \begin{align} 5x + 80 & = 180^\circ \\ 5x & = 180^\circ - 80^\circ \\ 5x & = 100^\circ \\ x & = 20^\circ \end{align} $
Jadi, nilai $ x = 20^\circ \, $ dan $ y = 11\frac{3}{7} ^\circ $ .
Demikian Soal dan Pembahasan Garis dan Sudut . Jika ada kekeliruan dalam penyelesaiannya, mohon kritik dan saranya agar penyelesaiannya menjadi lebih baik dengan memberikan komentar di kotak komentar di bawah. Semoga pembahasannya bisa bermanfaat untuk kita semua. Terima kasih.