Persamaan garis singgung lingkaran merupakan suatu garis yang menyinggung suatu lingkaran. Untuk memudahkan dalam mempelajari persamaan garis singgung lingkaran, sebaiknya baca dulu materi "persamaan lingkaran". Ada tiga jenis yang diketahui dalam menentukan persamaan garis singgung lingkaran, yaitu : Garis Singgung yang Melalui Suatu Titik pada Lingkaran, Garis Singgung Melalui Suatu Titik di Luar Lingkaran, dan garis singgung lingkaran yang diketahui gradien garisnya.
Contoh :
1). Tunjukkan bahwa titik (6, -8) terletak pada lingkaran $x^2 + y^2 = 100$, kemudian tentukan pula garis singgungnya.
Penyelesaian :
*). Menunjukkan bahwa titik (6, -8) terletak pada lingkaran $ x^2 + y^2 = 100 $ , substitusi titik tersebut ke persamaan lingkaran. Jika hasil ruas kiri sama dengan ruas kanan, maka titik tersebut dikatakan terletak pada lingkaran.
$\begin{align} (x,y) = (6,-8) \rightarrow x^2 + y^2 & = 100 \\ 6^2 + (-8)^2 & = 100 \\ 36 + 64 & = 100 \\ 100 & = 100 \end{align} $
Karena hasil ruas kiri sama dengan ruas kanan, maka titik (6,-8) terletak pada lingkaran $ x^2 + y^2 = 100 $ .
*). Menentukan persamaan garis singgung lingkaran
$\begin{align} (x_1,y_1) = (6,-8) \rightarrow x_1.x + y_1.y & = 100 \\ 6x +(-8)y & = 100 \\ 6x - 8y & = 100 \, \, \, \, \text{(bagi 2) } \\ 3x - 4y & = 50 \end{align} $
Jadi, PGS nya adalah $ 3x - 4y = 50 $
2). Tentukan persamaan garis singgung lingkaran $ (x + 2)^2 + (y - 3)^2 = 58 $ pada titik A(1, -4).
Penyelesaian :
*). Menentukan persamaan garis singgungnya di titik $(x_1,y_1)=(1,-4) $
$\begin{align} (x_1-a)(x-a) + (y_1 - b)(y-b) & = r^2 \\ (x_1+2)(x+2) + (y_1 - 3)(y-3) & = 58 \\ (1+2)(x+2) + (-4 - 3)(y-3) & = 58 \\ 3(x+2) + (-7)(y-3) & = 58 \\ 3x + 6 - 7y + 21 & = 58 \\ 3x - 7y & = 31 \end{align} $
Jadi, PGS nya adalah $ 3x - 7y = 31 $
3). Tentukan persamaan garis singgung lingkaran $ x^2 + y^2 -2x + 4y - 11 = 0 $ pada titik A(1, 2).
Penyelesaian :
*). Menentukan persamaan garis singgungnya di titik $(x_1,y_1)=(1,2) $
$\begin{align} x_1.x + y_1.y + A. \frac{(x_1+x)}{2} + B\frac{(y_1+y)}{2} + C & = 0 \\ x_1.x + y_1.y -2.\frac{(x_1+x)}{2} + 4.\frac{(y_1+y)}{2} - 11 & = 0 \\ 1.x + 2.y -2.\frac{(1+x)}{2} + 4.\frac{(2+y)}{2} - 11 & = 0 \\ x + 2y -(1+x) + 2(2+y) - 11 & = 0 \\ x + 2y -1 -x + 4 + 2y - 11 & = 0 \\ 4y - 8 & = 0 \\ 4y & = 8 \\ y & = 2 \end{align} $
Jadi, PGS nya adalah $ y = 2 $
Contoh :
Tentukan persamaan garis singgung melalui titik (7, 1) di luar lingkaran $ x^2 + y^2 = 25 $ !
Penyelesaian :
Cara I :
*). Titik (7, 1) berada di luar lingkaran $ x^2 + y^2 = 25 $ sebab jika titik (7, 1) disubstitusikan ke persamaan lingkaran tersebut diperoleh $ 7^2+1^2 = 49 + 1 = 50 > 25 $ .
*). Misalkan persamaan garis singgungnya : $ y = mx + n $
*). Titik (7,1) dilalui oleh garis singgung, sehingga bisa disubstitusi ke garis singgung :
$ \begin{align} (x,y)=(7,1) \rightarrow y & = mx + n \\ 1 & = m . 7 + n \\ n & = 1 - 7m \end{align} $
*). Substitusi bentuk $ n = 1 - 7m \, $ ke garis $ y = mx + n $
diperoleh garis singgung baru : $ y = mx + (1-7m) $
*). Substitusi garis singgung baru ke lingkaran :
$ \begin{align} y = mx + (1-7m) \rightarrow x^2 + y^2 & = 25 \\ x^2 + (mx + 1 - 7m)^2 & = 25 \\ x^2 + m^2x^2 -49m^2+1-14m^2x+2mx-14m & = 25 \\ (m^2+1)x^2 +(2m-14m^2)x + (-49m^2-14m-24) & = 0 \\ a = m^2 + 1, \, b = 2m - 14m^2 , \, c & = -49m^2-14m-24 \end{align} $
*). Menentukan nilai Diskriminan ($D$) :
$ \begin{align} D & = b^2 - 4ac \\ & = (2m-14m^2)^2 - 4.(m^2+1).(-49m^2-14m-24) \\ & = 4m^2 - 56m^3 + 196m^4 - 4(49m^2 - 14m - 24 + 49m^4 - 14m^3 - 24m^2) \\ & = -96m^2 + 56m + 96 \end{align} $
*). Syarat garis menyinggung lingkaran : $ D = 0 $
$ \begin{align} D & = 0 \\ -96m^2 + 56m + 96 & = 0 \, \, \, \, \text{(bagi -8)} \\ 12m^2 - 7m - 12 & = 0 \\ (4m + 3)(3m - 4) & = 0 \\ m = - \frac{3}{4} \vee m & = \frac{4}{3} \end{align} $
*). Substitusi nilai $ m \, $ ke garis singgung baru :
$ \begin{align} m = - \frac{3}{4} \rightarrow y & = mx + (1-7m) \\ y & = - \frac{3}{4} . x + (1-7.(- \frac{3}{4})) \\ y & = - \frac{3}{4} . x + (1 + \frac{21}{4}) \\ y & = - \frac{3}{4} . x + \frac{25}{4} \, \, \, \, \text{(kali 4)} \\ 4y & = -3x + 25 \\ 3x + 4y & = 25 \\ m = \frac{4}{3} \rightarrow y & = mx + (1-7m) \\ y & = \frac{4}{3} . x + (1-7.(\frac{4}{3})) \\ y & = \frac{4}{3} . x + (1 - \frac{28}{3}) \\ y & = \frac{4}{3} . x - \frac{25}{3} \, \, \, \, \text{(kali 3)} \\ 3y & = 4x - 25 \\ 4x - 3y & = 25 \end{align} $
Jadi, PGS nya adalah $ 3x + 4y = 25 \, $ dan $ 4x - 3y = 25 $ .
Cara II : Menggunakan garis kutub (polar)
*). Menentukan persamaan garis kutub di titik (7,1) :
$ \begin{align} x_1x + y_1y & = r^2 \\ 7.x + 1.y & = 25 \\ y & = 25 - 7x \\ y & = 25 - 7x \end{align} $
*). Substitusi $ y = 25 - 7x \, $ ke $ x^2 + y^2 = 25 $
$ \begin{align} x^2 + y^2 & = 25 \\ x^2 + (25 - 7x)^2 & = 25 \\ x^2 + 49x^2 - 350x + 625 & = 25 \\ x^2 + 49x^2 - 350x + 600 & = 0 \\ 50x^2 - 350x + 600 & = 0 \, \, \, \, \text{(bagi 50)} \\ x^2 - 7x + 12 & = 0 \\ (x - 3 )(x - 4 ) & = 0 \\ x = 3 \vee x & = 4 \end{align} $
*). Menentukan titik singgungnya :
$ \begin{align} x = 3 \rightarrow y & = 25 - 7x \\ y & = 25 - 7.3 \\ y & = 4 \\ x = 4 \rightarrow y & = 25 - 7x \\ y & = 25 - 7.4 \\ y & = -3 \end{align} $
Titik singgungnya : (3,4) dan 4,-3) .
*). Menentukan PGS dengan cara Bagi ADIL
titik $ (x_1,y_1) = (3,4) $
$ \begin{align} x^2 + y^2 & = 25 \\ x_1x + y_1y & = 25 \\ 3x + 4y & = 25 \end{align} $
titik $ (x_1,y_1) = (4,-3) $
$ \begin{align} x^2 + y^2 & = 25 \\ x_1x + y_1y & = 25 \\ 4x -3y & = 25 \end{align} $
Jadi, PGS nya adalah $ 3x + 4y = 25 \, $ dan $ 4x - 3y = 25 $ .
Contoh :
1). Tentukan persamaan garis singgung dengan gradien $ \sqrt{8} \, $ pada lingkaran $ x^2 + y^2 = 16 $ !
Penyelesaian :
*). Menentukan unsur-unsur lingkaran :
$ x^2 + y^2 = 16, \, $ jari-jari : $ r^2 = 16 \rightarrow r = 4 $
*). Menentukan PGS dengan gradien $ m = \sqrt{8} $
$\begin{align} y & = mx \pm r \sqrt{1 + m^2} \\ y & = \sqrt{8}x \pm 4 \sqrt{1 + (\sqrt{8})^2} \\ y & = \sqrt{8}x \pm 4 \sqrt{1 + 8} \\ y & = \sqrt{8}x \pm 4 . 3 \\ y & = \sqrt{8}x \pm 12 \end{align} $
Jadi, PGS nya adalah $ y = \sqrt{8}x + 12 \, $ dan $ y = \sqrt{8}x - 12 $
2). Tentukan persamaan garis singgung yang sejajar dengan garis $ y = 2x - 3 \, $ pada lingkaran $ (x-2)^2 + (y+1)^2 = 1 $ !
Penyelesaian :
*). Menentukan unsur-unsur lingkaran :
$ (x-2)^2 + (y+1)^2 = 1, \, $ jari-jari : $ r^2 = 1 \rightarrow r = 1 $
Pusatnya : $ (a,b) = (2, -1) $
*). Menentukan gradien garis singgungnya
Garis $ y = 2x - 3 \rightarrow m_1 = 2 $
Karena sejajar, maka gradiennya sama, sehingga $ m = 2 $
*). Menentukan PGS dengan gradien $ m = 2 $
$\begin{align} y - b & = m(x-a) \pm r \sqrt{1 + m^2} \\ y - (-1) & = 2(x - 2) \pm 1. \sqrt{1 + 2^2} \\ y + 1 & = 2x - 4 \pm \sqrt{5} \\ y & = 2x - 4 - 1 \pm \sqrt{5} \\ y & = 2x - 5 \pm \sqrt{5} \end{align} $
Jadi, PGS nya adalah $ y = 2x - 5 + \sqrt{5} \, $ dan $ y = 2x - 5 - \sqrt{5} $
3). Tentukan persamaan garis singgung yang tegak lurus dengan garis $ -3x + 4y - 1 = 0, \, $ pada lingkaran $ x^2 + y^2 + 4x - 2y + 1 = 0 $ !
Penyelesaian :
*). Menentukan unsur-unsur lingkaran :
$ x^2 + y^2 + 4x - 2y + 1 = 0, \rightarrow A = 4, B = -2, C = 1 $
Pusatnya : $ (a,b) = \left( -\frac{A}{2} , - \frac{B}{2} \right) = \left( -\frac{4}{2} , - \frac{-2}{2} \right) = (-2,1) $
Jari-jari : $ r = \sqrt{a^2 + b^2 - C} = \sqrt{(-2)^2 + 1^2 - 1} = 2 $
*). Menentukan gradien garis singgungnya
Garis $ -3x + 4y - 1 = 0 \rightarrow m_1 = -\frac{-3}{4} = \frac{3}{4} $
Karena tegak lurus, maka $ m.m_1 = -1 \rightarrow m . \frac{3}{4} = -1 \rightarrow m = - \frac{4}{3} $
*). Menentukan PGS dengan gradien $ m = - \frac{4}{3} $
$\begin{align} y - b & = m(x-a) \pm r \sqrt{1 + m^2} \\ y - 1 & = - \frac{4}{3}.(x - (-2)) \pm 2. \sqrt{1 + (- \frac{4}{3})^2} \\ y - 1 & = - \frac{4}{3}.(x + 2) \pm 2 \sqrt{1 + \frac{16}{9}} \\ y - 1 & = - \frac{4}{3}x - \frac{8}{3} \pm 2 \sqrt{ \frac{25}{9}} \\ y - 1 & = - \frac{4}{3}x - \frac{8}{3} \pm 2 . \frac{5}{3} \\ y - 1 & = - \frac{4}{3}x - \frac{8}{3} \pm \frac{10}{3} \, \, \, \, \text{(kali 3)} \\ 3y - 3 & = - 4x - 8 \pm 10 \\ 3y & = - 4x - 8 + 3 \pm 10 \\ 3y & = - 4x - 5 \pm 10 \\ \text{(PGS I) } : 3y & = - 4x - 5 + 10 \\ 3y & = -4x + 5 \\ 4x + 3y & = 5 \\ \text{(PGS II) } : 3y & = - 4x - 5 - 10 \\ 3y & = -4x - 15 \\ 4x + 3y & = -15 \end{align} $
Jadi, PGS nya adalah $ 4x + 3y = 5 \, $ dan $ 4x + 3y = -15 $
Persamaan Garis Singgung (PGS) yang Melalui Suatu Titik pada Lingkaran
Persamaan Garis Singgung yang Melalui Suatu Titik pada Lingkaran maksudnya titik yang dilalui oleh garis ada pada ingkaran. Berikut penjabarannya masing-masing
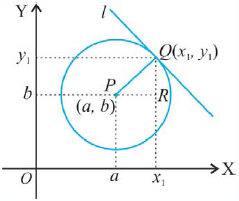
i). Persamaan Garis Singgung di Titik P($x_1, y_1$) pada
Lingkaran $x^2 + y^2 = r^2 $
Persamaan garis singgungnya : $ \begin{align} x_1.x + y_1.y = r^2 \end{align} $
ii). Persamaan Garis Singgung di Titik P($x_1, y_1$) pada
Lingkaran $(x-a)^2 + (y-b)^2 = r^2 $
Persamaan garis singgungnya :
$ \begin{align} (x_1-a)(x-a) + (y_1 - b)(y-b) = r^2 \end{align} $
iii). Persamaan Garis Singgung Melalui Titik Q($x_1, y_1$) pada
Lingkaran $x^2 + y^2 + Ax + By + C = 0$
Persamaan garis singgungnya :
$ x_1.x + y_1.y + A. \frac{(x_1+x)}{2} + B\frac{(y_1+y)}{2} + C = 0 $
Catatan : Cara ini dinamakan cara BAGI ADIL.
Untuk pembuktian rumus di atas, silahkan baca materi "Pembuktian Rumus Persamaan Garis Singgung Lingkaran".
i). Persamaan Garis Singgung di Titik P($x_1, y_1$) pada
Lingkaran $x^2 + y^2 = r^2 $
Persamaan garis singgungnya : $ \begin{align} x_1.x + y_1.y = r^2 \end{align} $
ii). Persamaan Garis Singgung di Titik P($x_1, y_1$) pada
Lingkaran $(x-a)^2 + (y-b)^2 = r^2 $
Persamaan garis singgungnya :
$ \begin{align} (x_1-a)(x-a) + (y_1 - b)(y-b) = r^2 \end{align} $
iii). Persamaan Garis Singgung Melalui Titik Q($x_1, y_1$) pada
Lingkaran $x^2 + y^2 + Ax + By + C = 0$
Persamaan garis singgungnya :
$ x_1.x + y_1.y + A. \frac{(x_1+x)}{2} + B\frac{(y_1+y)}{2} + C = 0 $
Catatan : Cara ini dinamakan cara BAGI ADIL.
Untuk pembuktian rumus di atas, silahkan baca materi "Pembuktian Rumus Persamaan Garis Singgung Lingkaran".
1). Tunjukkan bahwa titik (6, -8) terletak pada lingkaran $x^2 + y^2 = 100$, kemudian tentukan pula garis singgungnya.
Penyelesaian :
*). Menunjukkan bahwa titik (6, -8) terletak pada lingkaran $ x^2 + y^2 = 100 $ , substitusi titik tersebut ke persamaan lingkaran. Jika hasil ruas kiri sama dengan ruas kanan, maka titik tersebut dikatakan terletak pada lingkaran.
$\begin{align} (x,y) = (6,-8) \rightarrow x^2 + y^2 & = 100 \\ 6^2 + (-8)^2 & = 100 \\ 36 + 64 & = 100 \\ 100 & = 100 \end{align} $
Karena hasil ruas kiri sama dengan ruas kanan, maka titik (6,-8) terletak pada lingkaran $ x^2 + y^2 = 100 $ .
*). Menentukan persamaan garis singgung lingkaran
$\begin{align} (x_1,y_1) = (6,-8) \rightarrow x_1.x + y_1.y & = 100 \\ 6x +(-8)y & = 100 \\ 6x - 8y & = 100 \, \, \, \, \text{(bagi 2) } \\ 3x - 4y & = 50 \end{align} $
Jadi, PGS nya adalah $ 3x - 4y = 50 $
2). Tentukan persamaan garis singgung lingkaran $ (x + 2)^2 + (y - 3)^2 = 58 $ pada titik A(1, -4).
Penyelesaian :
*). Menentukan persamaan garis singgungnya di titik $(x_1,y_1)=(1,-4) $
$\begin{align} (x_1-a)(x-a) + (y_1 - b)(y-b) & = r^2 \\ (x_1+2)(x+2) + (y_1 - 3)(y-3) & = 58 \\ (1+2)(x+2) + (-4 - 3)(y-3) & = 58 \\ 3(x+2) + (-7)(y-3) & = 58 \\ 3x + 6 - 7y + 21 & = 58 \\ 3x - 7y & = 31 \end{align} $
Jadi, PGS nya adalah $ 3x - 7y = 31 $
3). Tentukan persamaan garis singgung lingkaran $ x^2 + y^2 -2x + 4y - 11 = 0 $ pada titik A(1, 2).
Penyelesaian :
*). Menentukan persamaan garis singgungnya di titik $(x_1,y_1)=(1,2) $
$\begin{align} x_1.x + y_1.y + A. \frac{(x_1+x)}{2} + B\frac{(y_1+y)}{2} + C & = 0 \\ x_1.x + y_1.y -2.\frac{(x_1+x)}{2} + 4.\frac{(y_1+y)}{2} - 11 & = 0 \\ 1.x + 2.y -2.\frac{(1+x)}{2} + 4.\frac{(2+y)}{2} - 11 & = 0 \\ x + 2y -(1+x) + 2(2+y) - 11 & = 0 \\ x + 2y -1 -x + 4 + 2y - 11 & = 0 \\ 4y - 8 & = 0 \\ 4y & = 8 \\ y & = 2 \end{align} $
Jadi, PGS nya adalah $ y = 2 $
Persamaan Garis Singgung Melalui Suatu Titik di Luar Lingkaran
Garis Singgung Melalui Suatu Titik di Luar Lingkaran maksudnya titik yang dilalui oleh garis singgung ada di luar lingkaran. Misalkan titik yang dilalui adalah titik A($x_1,y_1$). Dari titik yang dilalui tersebut bisa ditarik dua garis singgung melalui titik pada lingkaran misalnya B($x_2,y_2$) dan titik C($x_3,y_3$).
Ada dua cara menentukan persamaan garis singgungnya, yaitu :
$\clubsuit \, $ 1). Persamaan garis singgung melalui titik A($x_1,y_1$) diluar lingkaran,
Langkah-langkah penyelesaian :
i). Misalkan garis singggungnya $ y = mx + n $ ,
ii). Substitusi titik A($x_1,y_1$) ke garis $ y = mx + n $ , dan tentukan nilai $ n \, $ dalam bentuk $ m $ kemudian substitusi nilai $ n \, $ ke garis $ y = mx + n $ .
iii). Substitusi garis yang baru ke persamaan lingkaran, lalu tentukan nilai diskriminannya ($D$).
iv). Tentukan nilai $ m \, $ dengan syarat garis menyinggung lingkaran : $ D = 0 $ .
v). Substitusi nilai $ m $ yang diperoleh ke garis baru yang terbentuk.
$\clubsuit \, $ 2). Menggunakan garis kutub (polar).
Jika melalui titik A($x_1, y_1$) di luar lingkaran ditarik dua buah garis singgung pada lingkaran dengan titik singgungnya B($x_2, y_2$) dan C($x_3, y_3$), maka persamaan garis BC adalah $x_1.x + y_1.y = r^2$ disebut garis kutub pada lingkaran dan titik A($x_1, y_1$) disebut titik kutub.
Langkah-langkah penyelesaian :
i). Membuat persamaan garis kutub dari titik A($x_1, y_1$) terhadap lingkaran.
ii). Substitusi garis kutub yang terbentuk ke persamaan lingkaran, lalu selesaikan untuk menentukan nilai $ x \, $ .
iii). Substitusi nilai $ x \, $ atau $ y \, $ yang diperoleh ke persamaan garis kutub untuk menentukan titik B dan C.
iv). Titik B dan C adalah titik pada lingkaran yang dilalui oleh garis singgung, selanjutnya gunakan cara BAGI ADIL.
Ada dua cara menentukan persamaan garis singgungnya, yaitu :
$\clubsuit \, $ 1). Persamaan garis singgung melalui titik A($x_1,y_1$) diluar lingkaran,
Langkah-langkah penyelesaian :
i). Misalkan garis singggungnya $ y = mx + n $ ,
ii). Substitusi titik A($x_1,y_1$) ke garis $ y = mx + n $ , dan tentukan nilai $ n \, $ dalam bentuk $ m $ kemudian substitusi nilai $ n \, $ ke garis $ y = mx + n $ .
iii). Substitusi garis yang baru ke persamaan lingkaran, lalu tentukan nilai diskriminannya ($D$).
iv). Tentukan nilai $ m \, $ dengan syarat garis menyinggung lingkaran : $ D = 0 $ .
v). Substitusi nilai $ m $ yang diperoleh ke garis baru yang terbentuk.
$\clubsuit \, $ 2). Menggunakan garis kutub (polar).
Jika melalui titik A($x_1, y_1$) di luar lingkaran ditarik dua buah garis singgung pada lingkaran dengan titik singgungnya B($x_2, y_2$) dan C($x_3, y_3$), maka persamaan garis BC adalah $x_1.x + y_1.y = r^2$ disebut garis kutub pada lingkaran dan titik A($x_1, y_1$) disebut titik kutub.
Langkah-langkah penyelesaian :
i). Membuat persamaan garis kutub dari titik A($x_1, y_1$) terhadap lingkaran.
ii). Substitusi garis kutub yang terbentuk ke persamaan lingkaran, lalu selesaikan untuk menentukan nilai $ x \, $ .
iii). Substitusi nilai $ x \, $ atau $ y \, $ yang diperoleh ke persamaan garis kutub untuk menentukan titik B dan C.
iv). Titik B dan C adalah titik pada lingkaran yang dilalui oleh garis singgung, selanjutnya gunakan cara BAGI ADIL.
Tentukan persamaan garis singgung melalui titik (7, 1) di luar lingkaran $ x^2 + y^2 = 25 $ !
Penyelesaian :
Cara I :
*). Titik (7, 1) berada di luar lingkaran $ x^2 + y^2 = 25 $ sebab jika titik (7, 1) disubstitusikan ke persamaan lingkaran tersebut diperoleh $ 7^2+1^2 = 49 + 1 = 50 > 25 $ .
*). Misalkan persamaan garis singgungnya : $ y = mx + n $
*). Titik (7,1) dilalui oleh garis singgung, sehingga bisa disubstitusi ke garis singgung :
$ \begin{align} (x,y)=(7,1) \rightarrow y & = mx + n \\ 1 & = m . 7 + n \\ n & = 1 - 7m \end{align} $
*). Substitusi bentuk $ n = 1 - 7m \, $ ke garis $ y = mx + n $
diperoleh garis singgung baru : $ y = mx + (1-7m) $
*). Substitusi garis singgung baru ke lingkaran :
$ \begin{align} y = mx + (1-7m) \rightarrow x^2 + y^2 & = 25 \\ x^2 + (mx + 1 - 7m)^2 & = 25 \\ x^2 + m^2x^2 -49m^2+1-14m^2x+2mx-14m & = 25 \\ (m^2+1)x^2 +(2m-14m^2)x + (-49m^2-14m-24) & = 0 \\ a = m^2 + 1, \, b = 2m - 14m^2 , \, c & = -49m^2-14m-24 \end{align} $
*). Menentukan nilai Diskriminan ($D$) :
$ \begin{align} D & = b^2 - 4ac \\ & = (2m-14m^2)^2 - 4.(m^2+1).(-49m^2-14m-24) \\ & = 4m^2 - 56m^3 + 196m^4 - 4(49m^2 - 14m - 24 + 49m^4 - 14m^3 - 24m^2) \\ & = -96m^2 + 56m + 96 \end{align} $
*). Syarat garis menyinggung lingkaran : $ D = 0 $
$ \begin{align} D & = 0 \\ -96m^2 + 56m + 96 & = 0 \, \, \, \, \text{(bagi -8)} \\ 12m^2 - 7m - 12 & = 0 \\ (4m + 3)(3m - 4) & = 0 \\ m = - \frac{3}{4} \vee m & = \frac{4}{3} \end{align} $
*). Substitusi nilai $ m \, $ ke garis singgung baru :
$ \begin{align} m = - \frac{3}{4} \rightarrow y & = mx + (1-7m) \\ y & = - \frac{3}{4} . x + (1-7.(- \frac{3}{4})) \\ y & = - \frac{3}{4} . x + (1 + \frac{21}{4}) \\ y & = - \frac{3}{4} . x + \frac{25}{4} \, \, \, \, \text{(kali 4)} \\ 4y & = -3x + 25 \\ 3x + 4y & = 25 \\ m = \frac{4}{3} \rightarrow y & = mx + (1-7m) \\ y & = \frac{4}{3} . x + (1-7.(\frac{4}{3})) \\ y & = \frac{4}{3} . x + (1 - \frac{28}{3}) \\ y & = \frac{4}{3} . x - \frac{25}{3} \, \, \, \, \text{(kali 3)} \\ 3y & = 4x - 25 \\ 4x - 3y & = 25 \end{align} $
Jadi, PGS nya adalah $ 3x + 4y = 25 \, $ dan $ 4x - 3y = 25 $ .
Cara II : Menggunakan garis kutub (polar)
*). Menentukan persamaan garis kutub di titik (7,1) :
$ \begin{align} x_1x + y_1y & = r^2 \\ 7.x + 1.y & = 25 \\ y & = 25 - 7x \\ y & = 25 - 7x \end{align} $
*). Substitusi $ y = 25 - 7x \, $ ke $ x^2 + y^2 = 25 $
$ \begin{align} x^2 + y^2 & = 25 \\ x^2 + (25 - 7x)^2 & = 25 \\ x^2 + 49x^2 - 350x + 625 & = 25 \\ x^2 + 49x^2 - 350x + 600 & = 0 \\ 50x^2 - 350x + 600 & = 0 \, \, \, \, \text{(bagi 50)} \\ x^2 - 7x + 12 & = 0 \\ (x - 3 )(x - 4 ) & = 0 \\ x = 3 \vee x & = 4 \end{align} $
*). Menentukan titik singgungnya :
$ \begin{align} x = 3 \rightarrow y & = 25 - 7x \\ y & = 25 - 7.3 \\ y & = 4 \\ x = 4 \rightarrow y & = 25 - 7x \\ y & = 25 - 7.4 \\ y & = -3 \end{align} $
Titik singgungnya : (3,4) dan 4,-3) .
*). Menentukan PGS dengan cara Bagi ADIL
titik $ (x_1,y_1) = (3,4) $
$ \begin{align} x^2 + y^2 & = 25 \\ x_1x + y_1y & = 25 \\ 3x + 4y & = 25 \end{align} $
titik $ (x_1,y_1) = (4,-3) $
$ \begin{align} x^2 + y^2 & = 25 \\ x_1x + y_1y & = 25 \\ 4x -3y & = 25 \end{align} $
Jadi, PGS nya adalah $ 3x + 4y = 25 \, $ dan $ 4x - 3y = 25 $ .
Persamaan Garis Singgung (PGS) Lingkaran dengan gradien $ m $
Persamaan Garis Singgung (PGS) Lingkaran dengan gradien $ m $ kita bagi menjadi tiga berdasarkan jenis persamaan lingkarannya, yaitu :
i). Persamaan Garis Singgung dengan Gradien $ m $ terhadap Lingkaran $ x^2 + y^2 = r^2 $
Persamaan garis singgungnya : $ \begin{align} y = mx \pm r \sqrt{1 + m^2} \end{align} $
ii). Persamaan Garis Singgung dengan Gradien $ m $ terhadap Lingkaran $ (x-a)^2 + (y-b)^2 = r^2 $
Persamaan garis singgungnya : $ \begin{align} y - b = m(x-a) \pm r \sqrt{1 + m^2} \end{align} $
iii). Persamaan Garis Singgung dengan Gradien $ m $ terhadap Lingkaran $ x^2 + y^2 + Ax + By + C = 0 $
Persamaan garis singgungnya : $ \begin{align} y - b = m(x-a) \pm r \sqrt{1 + m^2} \end{align} $
Untuk menentukan pusat dan jari-jarinya, silahkan baca materi "Persamaan Lingkaran"
Karena ada kaitannya dengan gradien, maka biasanya juga melibatkan hubungan antara dua garis. Silahkan baca materi "Hubungan Dua Garis".
*). Dua garis sejajar, maka gradiennya sama : $ m_1 = m_2 $
*). Dua garis tegak lurus : $ m_1 . m_2 = -1 $
Untuk pembuktian rumus di atas, silahkan baca materi "Pembuktian Rumus Persamaan Garis Singgung Lingkaran".
i). Persamaan Garis Singgung dengan Gradien $ m $ terhadap Lingkaran $ x^2 + y^2 = r^2 $
Persamaan garis singgungnya : $ \begin{align} y = mx \pm r \sqrt{1 + m^2} \end{align} $
ii). Persamaan Garis Singgung dengan Gradien $ m $ terhadap Lingkaran $ (x-a)^2 + (y-b)^2 = r^2 $
Persamaan garis singgungnya : $ \begin{align} y - b = m(x-a) \pm r \sqrt{1 + m^2} \end{align} $
iii). Persamaan Garis Singgung dengan Gradien $ m $ terhadap Lingkaran $ x^2 + y^2 + Ax + By + C = 0 $
Persamaan garis singgungnya : $ \begin{align} y - b = m(x-a) \pm r \sqrt{1 + m^2} \end{align} $
Untuk menentukan pusat dan jari-jarinya, silahkan baca materi "Persamaan Lingkaran"
Karena ada kaitannya dengan gradien, maka biasanya juga melibatkan hubungan antara dua garis. Silahkan baca materi "Hubungan Dua Garis".
*). Dua garis sejajar, maka gradiennya sama : $ m_1 = m_2 $
*). Dua garis tegak lurus : $ m_1 . m_2 = -1 $
Untuk pembuktian rumus di atas, silahkan baca materi "Pembuktian Rumus Persamaan Garis Singgung Lingkaran".
1). Tentukan persamaan garis singgung dengan gradien $ \sqrt{8} \, $ pada lingkaran $ x^2 + y^2 = 16 $ !
Penyelesaian :
*). Menentukan unsur-unsur lingkaran :
$ x^2 + y^2 = 16, \, $ jari-jari : $ r^2 = 16 \rightarrow r = 4 $
*). Menentukan PGS dengan gradien $ m = \sqrt{8} $
$\begin{align} y & = mx \pm r \sqrt{1 + m^2} \\ y & = \sqrt{8}x \pm 4 \sqrt{1 + (\sqrt{8})^2} \\ y & = \sqrt{8}x \pm 4 \sqrt{1 + 8} \\ y & = \sqrt{8}x \pm 4 . 3 \\ y & = \sqrt{8}x \pm 12 \end{align} $
Jadi, PGS nya adalah $ y = \sqrt{8}x + 12 \, $ dan $ y = \sqrt{8}x - 12 $
2). Tentukan persamaan garis singgung yang sejajar dengan garis $ y = 2x - 3 \, $ pada lingkaran $ (x-2)^2 + (y+1)^2 = 1 $ !
Penyelesaian :
*). Menentukan unsur-unsur lingkaran :
$ (x-2)^2 + (y+1)^2 = 1, \, $ jari-jari : $ r^2 = 1 \rightarrow r = 1 $
Pusatnya : $ (a,b) = (2, -1) $
*). Menentukan gradien garis singgungnya
Garis $ y = 2x - 3 \rightarrow m_1 = 2 $
Karena sejajar, maka gradiennya sama, sehingga $ m = 2 $
*). Menentukan PGS dengan gradien $ m = 2 $
$\begin{align} y - b & = m(x-a) \pm r \sqrt{1 + m^2} \\ y - (-1) & = 2(x - 2) \pm 1. \sqrt{1 + 2^2} \\ y + 1 & = 2x - 4 \pm \sqrt{5} \\ y & = 2x - 4 - 1 \pm \sqrt{5} \\ y & = 2x - 5 \pm \sqrt{5} \end{align} $
Jadi, PGS nya adalah $ y = 2x - 5 + \sqrt{5} \, $ dan $ y = 2x - 5 - \sqrt{5} $
3). Tentukan persamaan garis singgung yang tegak lurus dengan garis $ -3x + 4y - 1 = 0, \, $ pada lingkaran $ x^2 + y^2 + 4x - 2y + 1 = 0 $ !
Penyelesaian :
*). Menentukan unsur-unsur lingkaran :
$ x^2 + y^2 + 4x - 2y + 1 = 0, \rightarrow A = 4, B = -2, C = 1 $
Pusatnya : $ (a,b) = \left( -\frac{A}{2} , - \frac{B}{2} \right) = \left( -\frac{4}{2} , - \frac{-2}{2} \right) = (-2,1) $
Jari-jari : $ r = \sqrt{a^2 + b^2 - C} = \sqrt{(-2)^2 + 1^2 - 1} = 2 $
*). Menentukan gradien garis singgungnya
Garis $ -3x + 4y - 1 = 0 \rightarrow m_1 = -\frac{-3}{4} = \frac{3}{4} $
Karena tegak lurus, maka $ m.m_1 = -1 \rightarrow m . \frac{3}{4} = -1 \rightarrow m = - \frac{4}{3} $
*). Menentukan PGS dengan gradien $ m = - \frac{4}{3} $
$\begin{align} y - b & = m(x-a) \pm r \sqrt{1 + m^2} \\ y - 1 & = - \frac{4}{3}.(x - (-2)) \pm 2. \sqrt{1 + (- \frac{4}{3})^2} \\ y - 1 & = - \frac{4}{3}.(x + 2) \pm 2 \sqrt{1 + \frac{16}{9}} \\ y - 1 & = - \frac{4}{3}x - \frac{8}{3} \pm 2 \sqrt{ \frac{25}{9}} \\ y - 1 & = - \frac{4}{3}x - \frac{8}{3} \pm 2 . \frac{5}{3} \\ y - 1 & = - \frac{4}{3}x - \frac{8}{3} \pm \frac{10}{3} \, \, \, \, \text{(kali 3)} \\ 3y - 3 & = - 4x - 8 \pm 10 \\ 3y & = - 4x - 8 + 3 \pm 10 \\ 3y & = - 4x - 5 \pm 10 \\ \text{(PGS I) } : 3y & = - 4x - 5 + 10 \\ 3y & = -4x + 5 \\ 4x + 3y & = 5 \\ \text{(PGS II) } : 3y & = - 4x - 5 - 10 \\ 3y & = -4x - 15 \\ 4x + 3y & = -15 \end{align} $
Jadi, PGS nya adalah $ 4x + 3y = 5 \, $ dan $ 4x + 3y = -15 $