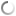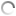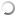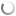Garis istimewa segitiga terakhir yang kita bahas kali ini adalah garis bagi. Pada materi Panjang Garis Bagi pada Segitiga dan Pembuktiannya ini kita akan membahas teorinya, contoh-contoh soal, dan tentu pembuktiannya rumus yang ada yang berkaitan dengan panjang garis bagi. Silahkan baca juga materi "Dalil Stewart" dan "aturan cosinus" yang digunakan untuk membuktikan rumus panjang garis bagi ini.
Penyelesaian :
*). Ilustrasi gambar segitiga ABC dan garis bagi AD.
*). Dengan pythagoras, maka kita peroleh panjang BC = 5 cm.
*). Menentukan panjang $ m \, $ dan $ n $.
$ \frac{m}{n} = \frac{3}{4} $, dari perbandingan ini maka,
$ m = \frac{3}{7}.BC = \frac{3}{7}.5 = \frac{15}{7} $.
$ n = \frac{4}{7}.BC = \frac{4}{7}.5 = \frac{20}{7} $.
*). Menentukan panjang AD,
$ \begin{align} d^2 & = bc - mn \\ & = 4.3 - \frac{15}{7} . \frac{20}{7} \\ & = 12 - \frac{300}{49} \\ & = \frac{588}{49} - \frac{300}{49} \\ d^2 & = \frac{288}{49} \\ d & = \sqrt{\frac{144.2}{49} } \\ d & = \frac{12}{7}\sqrt{2} \end{align} $
Jadi, panjang garis bagi $ AD = d = \frac{12}{7}\sqrt{2} \, $ cm.
2). Sebuah segitiga ABC dengan AB = 21 cm, BC = 18 cm, dan AC = 12 cm. CD adalah garis bagi. E adalah titik tengah BC. Hitunglah panjang DE!
Penyelesaian :
*). Ilustrasi gambarnya,
*). Menentukan panjang garis bagi CD.
Perbandingan : $ \frac{m}{n} = \frac{18}{12} = \frac{3}{2} $,
Sehingga $ m = \frac{3}{5}AB = \frac{3}{5}.21 = \frac{63}{5} $
dan $ DB = n = \frac{2}{5}AB = \frac{2}{5}.21 = \frac{42}{5} $
Panjang CD :
$ \begin{align} CD^2 & = CA.CB - mn \\ CD^2 & = 12.18 - \frac{63}{5} . \frac{42}{5} \\ CD^2 & = \frac{2754}{25} \end{align} $
*). Titik E ada di tengah BC, artinya DE adalah garis berat pada segitiga BDC.
Panjang garis berat DE pada segitiga BDC,
$ \begin{align} DE^2 & = \frac{1}{2}.CD^2 + \frac{1}{2}.DB^2 - \frac{1}{4}.BC^2 \\ DE^2 & = \frac{1}{2}. \frac{2754}{25} + \frac{1}{2}. (\frac{42}{5})^2 - \frac{1}{4}.12^2 \\ DE^2 & = \frac{1377}{25} + \frac{882}{25} - 36 \\ DE^2 & = \frac{2259}{25} - 36 \\ DE^2 & = \frac{2259}{25} - \frac{900}{25} \\ DE^2 & = \frac{1359}{25} = \frac{9 . 151}{25} \\ DE & = \sqrt{ \frac{9 . 151}{25} } \\ DE & = \frac{3}{5}\sqrt{ 151} \end{align} $
Jadi, panjang $ DE = \frac{3}{5}\sqrt{ 151} \, $ cm.
3). Diketahui segitiga ABC dengan panjang AB = 3 cm dan BC = 6 cm. Jika garis berat AD, garis bagi BE, dan garis tinggi CF berpotongan pada satu titik O, maka tentukan panjang AC!
Penyelesaian :
*). Ilustrasi gambar segitiga ABC,
*). Garis BE adalah garis bagi, sehingga perbandingan AE : EC ,
$ \frac{AE}{EC} = \frac{AB}{BC} = \frac{3}{6} = \frac{1}{2} $.
*). Ketiga garis berptongan pada satu titik, maka berlaku dalil Ceva pada segitiga ABC,
$ \begin{align} \frac{AF}{FB}. \frac{BD}{DC} . \frac{CE}{EA} & = 1 \\ \frac{AF}{FB}. 1 . \frac{2}{1} & = 1 \\ \frac{AF}{FB} & = \frac{1}{2} \end{align} $
Dari perbandingan AF : FB = 1 : 2, maka
$ AF = \frac{1}{3} AB = \frac{1}{3}. 3 = 1 $
dan $ FB = \frac{2}{3} AB = \frac{2}{3}. 3 = 2 $
*). Gari CF adalah garis tinggi, sehingga berlaku dalil proyeksi garis tingi CF,
$ \begin{align} BC^2 & = AC^2 + AB^2 - 2.AF.AB \\ 6^2 & = AC^2 + 3^2 - 2.1.3 \\ 36 & = AC^2 + 9 - 6 \\ AC^2 & = 33 \\ AC & = \sqrt{33} \end{align} $
Jadi, panjang $ AC = \sqrt{33} \, $ cm.
Menentukan Panjang Garis Bagi pada Segitiga
Garis bagi sebuah segitiga adalah garis yang ditarik dari titik sudut segitiga memotong sisi didepan titik sudut tersebut dengan membagi dua sama besar suudut tersebut, seperti gambar berikut.
Dalil-dalil yang berlaku pada garis bagi segitiga yaitu :
1). Garis bagi segitiga (garis AD,BE,dan CF) berpotongan pada satu titik yang disebut titik bagi (titik O).
2). Garis bagi sudut sebuah segitiga membagi sisi yang didepannya menjadi dua bagian yang rasio panjangnya sama dengan rasio sisi-sisi yang berdekatan dengan bagian tersebut, perbandingan yang dimaksud yaitu $ BD : DC = AB : AC $.
3). Titik bagi sebuah segitiga merupakan titik pusat lingkaran dalam segitiga seperti gambar berikut.
4). Menentukan panjang garis bagi dengan rumus berikut,
Menentukan panjang garis bagi.
perhatikan gambar garis bagi berikut,
Misalkan panjang garis bagi $ AD = d , \, $
menentukan panjang $ d \, $ dengan rumus : $ \, d^2 = bc - mn $
dengan $ m : n = c : b $
sehingga $ m = \frac{c}{ b+ c} \times a \, $ dan $ n = \frac{b}{ b+ c} \times a $
1). Garis bagi segitiga (garis AD,BE,dan CF) berpotongan pada satu titik yang disebut titik bagi (titik O).
2). Garis bagi sudut sebuah segitiga membagi sisi yang didepannya menjadi dua bagian yang rasio panjangnya sama dengan rasio sisi-sisi yang berdekatan dengan bagian tersebut, perbandingan yang dimaksud yaitu $ BD : DC = AB : AC $.
3). Titik bagi sebuah segitiga merupakan titik pusat lingkaran dalam segitiga seperti gambar berikut.
Menentukan panjang garis bagi.
perhatikan gambar garis bagi berikut,
menentukan panjang $ d \, $ dengan rumus : $ \, d^2 = bc - mn $
dengan $ m : n = c : b $
sehingga $ m = \frac{c}{ b+ c} \times a \, $ dan $ n = \frac{b}{ b+ c} \times a $
Contoh soal garis bagi segitiga :
1). Segitiga ABC siku-siku di A dengan panjang AB = 3 cm dan BC = 4 cm. Dari titik sudut A ditarik garis bagi AD. Tentukan panjang AD!Penyelesaian :
*). Ilustrasi gambar segitiga ABC dan garis bagi AD.
*). Menentukan panjang $ m \, $ dan $ n $.
$ \frac{m}{n} = \frac{3}{4} $, dari perbandingan ini maka,
$ m = \frac{3}{7}.BC = \frac{3}{7}.5 = \frac{15}{7} $.
$ n = \frac{4}{7}.BC = \frac{4}{7}.5 = \frac{20}{7} $.
*). Menentukan panjang AD,
$ \begin{align} d^2 & = bc - mn \\ & = 4.3 - \frac{15}{7} . \frac{20}{7} \\ & = 12 - \frac{300}{49} \\ & = \frac{588}{49} - \frac{300}{49} \\ d^2 & = \frac{288}{49} \\ d & = \sqrt{\frac{144.2}{49} } \\ d & = \frac{12}{7}\sqrt{2} \end{align} $
Jadi, panjang garis bagi $ AD = d = \frac{12}{7}\sqrt{2} \, $ cm.
2). Sebuah segitiga ABC dengan AB = 21 cm, BC = 18 cm, dan AC = 12 cm. CD adalah garis bagi. E adalah titik tengah BC. Hitunglah panjang DE!
Penyelesaian :
*). Ilustrasi gambarnya,
Perbandingan : $ \frac{m}{n} = \frac{18}{12} = \frac{3}{2} $,
Sehingga $ m = \frac{3}{5}AB = \frac{3}{5}.21 = \frac{63}{5} $
dan $ DB = n = \frac{2}{5}AB = \frac{2}{5}.21 = \frac{42}{5} $
Panjang CD :
$ \begin{align} CD^2 & = CA.CB - mn \\ CD^2 & = 12.18 - \frac{63}{5} . \frac{42}{5} \\ CD^2 & = \frac{2754}{25} \end{align} $
*). Titik E ada di tengah BC, artinya DE adalah garis berat pada segitiga BDC.
Panjang garis berat DE pada segitiga BDC,
$ \begin{align} DE^2 & = \frac{1}{2}.CD^2 + \frac{1}{2}.DB^2 - \frac{1}{4}.BC^2 \\ DE^2 & = \frac{1}{2}. \frac{2754}{25} + \frac{1}{2}. (\frac{42}{5})^2 - \frac{1}{4}.12^2 \\ DE^2 & = \frac{1377}{25} + \frac{882}{25} - 36 \\ DE^2 & = \frac{2259}{25} - 36 \\ DE^2 & = \frac{2259}{25} - \frac{900}{25} \\ DE^2 & = \frac{1359}{25} = \frac{9 . 151}{25} \\ DE & = \sqrt{ \frac{9 . 151}{25} } \\ DE & = \frac{3}{5}\sqrt{ 151} \end{align} $
Jadi, panjang $ DE = \frac{3}{5}\sqrt{ 151} \, $ cm.
3). Diketahui segitiga ABC dengan panjang AB = 3 cm dan BC = 6 cm. Jika garis berat AD, garis bagi BE, dan garis tinggi CF berpotongan pada satu titik O, maka tentukan panjang AC!
Penyelesaian :
*). Ilustrasi gambar segitiga ABC,
$ \frac{AE}{EC} = \frac{AB}{BC} = \frac{3}{6} = \frac{1}{2} $.
*). Ketiga garis berptongan pada satu titik, maka berlaku dalil Ceva pada segitiga ABC,
$ \begin{align} \frac{AF}{FB}. \frac{BD}{DC} . \frac{CE}{EA} & = 1 \\ \frac{AF}{FB}. 1 . \frac{2}{1} & = 1 \\ \frac{AF}{FB} & = \frac{1}{2} \end{align} $
Dari perbandingan AF : FB = 1 : 2, maka
$ AF = \frac{1}{3} AB = \frac{1}{3}. 3 = 1 $
dan $ FB = \frac{2}{3} AB = \frac{2}{3}. 3 = 2 $
*). Gari CF adalah garis tinggi, sehingga berlaku dalil proyeksi garis tingi CF,
$ \begin{align} BC^2 & = AC^2 + AB^2 - 2.AF.AB \\ 6^2 & = AC^2 + 3^2 - 2.1.3 \\ 36 & = AC^2 + 9 - 6 \\ AC^2 & = 33 \\ AC & = \sqrt{33} \end{align} $
Jadi, panjang $ AC = \sqrt{33} \, $ cm.
Pembuktian dalil (2) garis bagi segitiga
Dalil (2) garis berat berbunyi :
Garis bagi sudut sebuah segitiga membagi sisi yang didepannya menjadi dua bagian yang rasio panjangnya sama dengan rasio sisi-sisi yang berdekatan dengan bagian tersebut, perbandingan yang dimaksud yaitu $ BD : DC = AB : AC $.
Perhatikan gambar segitiga garis begi berikut,
Kita tarik garis tinggi dari titik D yaitu garis tinggi DE dan DF.
*). Perhatikan segitiga ADF dan segitiga ADE,
Sudut FAD = sudut EAD (sudut sama),
Sudut AFD = sudut AED (sudut sama),
Sisi AD beripit pada kedua segitiga (sisi sama).
Karena memenuhi sudut-sudut-sisi (yang sama pada kedua segitiga), maka segitiga ADF dan segitiga ADE kongruen (bentuk dan ukuran sama). Sehingga panjang garis tinggi DE = DF.
*). Perhatikan segitiga ABD dan segitiga ACD,
Perbandingan luasnya : ingat DE = DF,
$ \frac{\text{Luas ABD}}{\text{Luas ACD}} = \frac{\frac{1}{2}AB.DF}{\frac{1}{2}AC.DF} = \frac{AB}{AC} \, $ ....pers(i)
*). Segitiga ABD dengan alas BD dan segitiga ACD dengan alas DC mempunyai tinggi yang sama, misalkan $ t_1 $.
$ \frac{\text{Luas ABD}}{\text{Luas ACD}} = \frac{\frac{1}{2}BD.t_1}{\frac{1}{2}DC.t_1} = \frac{BD}{DC} = \frac{m}{n} \, $ ....pers(ii)
Dari pers(i) dan pers(ii) kita peroleh : $ \frac{m}{n} = \frac{AB}{AC} \, $ atau $ \frac{m}{n} = \frac{c}{b} $.
Jadi terbukti untuk dalil (2) garis bagi segitiga.
Garis bagi sudut sebuah segitiga membagi sisi yang didepannya menjadi dua bagian yang rasio panjangnya sama dengan rasio sisi-sisi yang berdekatan dengan bagian tersebut, perbandingan yang dimaksud yaitu $ BD : DC = AB : AC $.
Perhatikan gambar segitiga garis begi berikut,
*). Perhatikan segitiga ADF dan segitiga ADE,
Sudut FAD = sudut EAD (sudut sama),
Sudut AFD = sudut AED (sudut sama),
Sisi AD beripit pada kedua segitiga (sisi sama).
Karena memenuhi sudut-sudut-sisi (yang sama pada kedua segitiga), maka segitiga ADF dan segitiga ADE kongruen (bentuk dan ukuran sama). Sehingga panjang garis tinggi DE = DF.
*). Perhatikan segitiga ABD dan segitiga ACD,
Perbandingan luasnya : ingat DE = DF,
$ \frac{\text{Luas ABD}}{\text{Luas ACD}} = \frac{\frac{1}{2}AB.DF}{\frac{1}{2}AC.DF} = \frac{AB}{AC} \, $ ....pers(i)
*). Segitiga ABD dengan alas BD dan segitiga ACD dengan alas DC mempunyai tinggi yang sama, misalkan $ t_1 $.
$ \frac{\text{Luas ABD}}{\text{Luas ACD}} = \frac{\frac{1}{2}BD.t_1}{\frac{1}{2}DC.t_1} = \frac{BD}{DC} = \frac{m}{n} \, $ ....pers(ii)
Dari pers(i) dan pers(ii) kita peroleh : $ \frac{m}{n} = \frac{AB}{AC} \, $ atau $ \frac{m}{n} = \frac{c}{b} $.
Jadi terbukti untuk dalil (2) garis bagi segitiga.
Pembuktian Panjang Garis Bagi dengan Aturan Cosinus
Untuk materi aturan cosinus, silahkan baca langsung materinya pada artikel "Penerapan Trigonometri pada Segitiga : Aturan Sinus, Aturan Cosinus, Luas Segitiga".
Perhatikan segitiga ABC berikut.
Besar sudut BAD = sudut CAD = $ x $.
Perbandingan sisi : $ \frac{m}{n} = \frac{c}{b} \rightarrow bm = cn \, $ ....pers(i).
*). Aturan Cosinus pada segitiga ABD,
$ m^2 = d^2 + c^2 - 2.d.c .\cos x , \, $ kalikan $ b $ kedua ruas,
$ \rightarrow b.m^2 = b.d^2 + b.c^2 - 2.b.d.c .\cos x \, $ ....pers(ii).
*). Aturan Cosinus pada segitiga ACD,
$ n^2 = d^2 + b^2 - 2.d.b .\cos x , \, $ kalikan $ c $ kedua ruas,
$ \rightarrow c.n^2 = c.d^2 + c.b^2 - 2.d.b .c.\cos x \, $ ....pers(iii).
*). Eliminasi pers(ii) dan pers(iii) :
$ \begin{array}{cc} b.m^2 = b.d^2 + b.c^2 - 2.b.d.c .\cos x & \\ c.n^2 = c.d^2 + c.b^2 - 2.d.b .c.\cos x & - \\ \hline b.m^2 - c.n^2 = d^2(b-c) - bc(b-c) & \end{array} $
Substitusi bentuk pers(i) : $ bm = cn $
$ \begin{align} b.m^2 - c.n^2 & = d^2(b-c) - bc(b-c) \\ (bm).m - (cn).n & = d^2(b-c) - bc(b-c) \\ (cn).m - (bm).n & = d^2(b-c) - bc(b-c) \\ -mn(b-c) & = d^2(b-c) - bc(b-c) \, \, \, \, \, \text{(bagi dg } b-c) \\ -mn & = d^2 - bc \\ d^2 & = bc - mn \end{align} $
Jadi, terbukti panjang garis bagi $ \, AD = d \, $ adalah
$ d^2 = bc - mn $ .
Perhatikan segitiga ABC berikut.
Perbandingan sisi : $ \frac{m}{n} = \frac{c}{b} \rightarrow bm = cn \, $ ....pers(i).
*). Aturan Cosinus pada segitiga ABD,
$ m^2 = d^2 + c^2 - 2.d.c .\cos x , \, $ kalikan $ b $ kedua ruas,
$ \rightarrow b.m^2 = b.d^2 + b.c^2 - 2.b.d.c .\cos x \, $ ....pers(ii).
*). Aturan Cosinus pada segitiga ACD,
$ n^2 = d^2 + b^2 - 2.d.b .\cos x , \, $ kalikan $ c $ kedua ruas,
$ \rightarrow c.n^2 = c.d^2 + c.b^2 - 2.d.b .c.\cos x \, $ ....pers(iii).
*). Eliminasi pers(ii) dan pers(iii) :
$ \begin{array}{cc} b.m^2 = b.d^2 + b.c^2 - 2.b.d.c .\cos x & \\ c.n^2 = c.d^2 + c.b^2 - 2.d.b .c.\cos x & - \\ \hline b.m^2 - c.n^2 = d^2(b-c) - bc(b-c) & \end{array} $
Substitusi bentuk pers(i) : $ bm = cn $
$ \begin{align} b.m^2 - c.n^2 & = d^2(b-c) - bc(b-c) \\ (bm).m - (cn).n & = d^2(b-c) - bc(b-c) \\ (cn).m - (bm).n & = d^2(b-c) - bc(b-c) \\ -mn(b-c) & = d^2(b-c) - bc(b-c) \, \, \, \, \, \text{(bagi dg } b-c) \\ -mn & = d^2 - bc \\ d^2 & = bc - mn \end{align} $
Jadi, terbukti panjang garis bagi $ \, AD = d \, $ adalah
$ d^2 = bc - mn $ .
Pembuktian Panjang Garis Bagi dengan Dalil Stewart
Perhatikan segitiga ABC berikut.
Perbandingan sisi : $ \frac{m}{n} = \frac{c}{b} \rightarrow bm = cn. $
dan panjang $ m + n = a $ .
*). Dalil Stewart pada segitiga ABC dan substitusi $ bm = cn $.
$ \begin{align} d^2 . a & = m.b^2 + n.c^2 - m.n.a \\ d^2 . a & = (bm).b + (cn).c - m.n.a \\ d^2 . a & = (cn).b + (bm).c - m.n.a \\ d^2 . a & = bc(m+n) - m.n.a \\ d^2 . a & = bc.a - m.n.a \, \, \, \, \, \text{(bagi dg } a) \\ d^2 & = bc - mn \end{align} $
Jadi, terbukti panjang garis bagi $ \, AD = d \, $ adalah
$ d^2 = bc - mn $ .
dan panjang $ m + n = a $ .
*). Dalil Stewart pada segitiga ABC dan substitusi $ bm = cn $.
$ \begin{align} d^2 . a & = m.b^2 + n.c^2 - m.n.a \\ d^2 . a & = (bm).b + (cn).c - m.n.a \\ d^2 . a & = (cn).b + (bm).c - m.n.a \\ d^2 . a & = bc(m+n) - m.n.a \\ d^2 . a & = bc.a - m.n.a \, \, \, \, \, \text{(bagi dg } a) \\ d^2 & = bc - mn \end{align} $
Jadi, terbukti panjang garis bagi $ \, AD = d \, $ adalah
$ d^2 = bc - mn $ .